Hostname: page-component-76c49bb84f-kjkt6 Total loading time: 0 Render date: 2025-07-06T01:10:30.779Z Has data issue: false hasContentIssue false
  • English
  • Français

On quantification with a finite universe

Published online by Cambridge University Press:  12 March 2014

Saharon Shelah
Saharon Shelah*
Affiliation:
Institute of Mathematics, The Hebrew University, Jerusalem, Israel Rutgers University, Mathematics Department, New Brunswick, New Jersey, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a finite universe (more exactly—a family 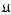of them), second order quantifiers QK, where for each this means quantifying over a family of n(K)-place relations closed under permuting . We define some natural orders and shed some light on the classification problem of those quantifiers.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 65 , Issue 3 , September 2000 , pp. 1055 - 1075
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Baldwin, John T., Definable second order quantifiers, Model theoretic logics (Barwise, J. and Feferman, S., editors), Perspectives in Mathematical Logic, Springer-Verlag, New York, Berlin, Heidelberg, and Tokyo, 1985, pp. 446–478.Google Scholar
[2]Baldwin, John T. and Shelah, Saharon, Second-order quantifiers and the complexity of theories, Notre Dame Journal of Formal Logic, vol. 26 (1985), pp. 229–303, Proceedings of the 1980/1 Jerusalem Model Theory year.CrossRefGoogle Scholar
[3]Shelah, Saharon, Non-structure theory, accepted, Oxford University Press.Google Scholar
[4]Shelah, Saharon, On quantification with a finite universe II.Google Scholar
[5]Shelah, Saharon, There are just four second-order quantifiers, Israel Journal of Mathematics, vol. 15 (1973), pp. 282–300.CrossRefGoogle Scholar
[6]Shelah, Saharon, Classifying of generalized quantifiers, Around classification theory of models, Lecture Notes in Mathematics, no. 1182, Springer-Verlag, Berlin, 1986, pp. 1–46.CrossRefGoogle Scholar