Article contents
On the structure of Ext(A,Z) in ZFC+
Published online by Cambridge University Press: 12 March 2014
Extract
A fundamental problem in the theory of abelian groups is to determine the structure of Ext(A, Z) for arbitrary abelian groups A. This problem was raised by L. Fuchs in 1958, and since then has been the center of considerable activity and progress.
We briefly summarize the present state of this problem. It is a well-known fact that
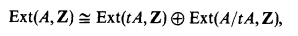
where tA denotes the torsion subgroup of A. Thus the structure problem for Ext(A, Z) breakdown to the two distinct cases, torsion and torsion free groups. For a torsion group T,

which is compact and reduced, and its structure is known explicitly [12].
For torsion free A, Ext(A, Z) is divisible; hence it has a unique representation
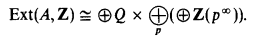
Thus Ext(A, Z) is characterized by countably many cardinal numbers, which we denote as follows: ν0(A) is the rank of the torsion free part of Ext(A, Z), and νp(A) are the ranks of the p-primary parts of Ext(A, Z), Extp(A, Z).
If A is free it is an elementary fact that Ext(A, Z) = 0. The second named author has shown [16] that in the presence of V = L the converse is also true. For countable torsion free, nonfree A, C. Jensen [13] has shown that νp(A) is either finite or  and νp(A) ≤ ν0(A). Therefore, the case for uncountable, nonfree, torsion free groups A remains to be studied.
and νp(A) ≤ ν0(A). Therefore, the case for uncountable, nonfree, torsion free groups A remains to be studied.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
- 27
- Cited by

