Hostname: page-component-77c89778f8-fv566 Total loading time: 0 Render date: 2024-07-19T03:27:40.874Z Has data issue: false hasContentIssue false
  • English
  • Français

POSITIONAL STRATEGIES IN LONG EHRENFEUCHT–FRAÏSSÉ GAMES

Published online by Cambridge University Press:  13 March 2015

S. SHELAH ,
J. VÄÄNÄNEN  and
B. VELIČKOVIĆ
S. SHELAH
Affiliation:
INSTITUTE OF MATHEMATICS, HEBREW UNIVERSITY, JERUSALEM ISRAEL AND DEPARTMENT OF MATHEMATICS, RUTGERS UNIVERSITY, NEW BRUNSWICK, NJ, USAE-mail: shelah@math.huji.ac.ilURL: http://shelah.logic.at
J. VÄÄNÄNEN
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS, UNIVERSITY OF HELSINKI, FINLAND AND INSTITUTE FOR LOGIC, LANGUAGE AND COMPUTATION UNIVERSITY OF AMSTERDAM, THE NETHERLANDSE-mail: jouko.vaananen@helsinki.fiURL: http://www.math.helsinki.fi/logic/people/jouko.vaananen
B. VELIČKOVIĆ
Affiliation:
EQUIPE DE LOGIQUE MATHÉMATIQUE, INSTITUT DE MATHÉMATIQUES DE JUSSIEU, UNIVERSITÉ PARIS DIDEROT, PARIS, FRANCEE-mail: boban@math.univ-paris-diderot.frURL: http://www.logique.jussieu.fr/∼boban
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that it is relatively consistent with ZF + CH that there exist two models of cardinality 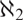$\aleph _2 $ such that the second player has a winning strategy in the Ehrenfeucht–Fraïssé-game of length ω1 but there is no σ-closed back-and-forth set for the two models. If CH fails, no such pairs of models exist.

Keywords

Ehrenfeucht-Fraisse gamepartial isomorphismmorass
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 1 , March 2015 , pp. 285 - 300
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Dickmann, M. A., Large infinitary languages, Model theory, Studies in Logic and the Foundations of Mathematics, vol. 83, North-Holland, Amsterdam, 1975.Google Scholar
Dickmann, M. A., Deux applications de la méthode de va-et-vient. Publ. Dép. Math. (Lyon), vol. 14 (1977), no. 2, pp. 63–92.Google Scholar
Erdös, P., Gillman, L., and Henriksen, M., An isomorphism theorem for real-closed fields. Annals of Mathematics (2), vol. 61 (1955), pp. 542–554.CrossRefGoogle Scholar
Hyttinen, Tapani, Games and infinitary languages. Ann. Acad. Sci. Fenn. Ser. A I Math. Dissertationes, vol. 64 (1987), p. 32.Google Scholar
Karttunen, Maaret, Infinitary languages N ∞λand generalized partial isomorphisms. Essays on mathematical and philosophical logic (Proc. Fourth Scandinavian Logic Sympos. and First Soviet-Finnish Logic Conf., Jyväskylä, 1976), Synthese Library, vol. 122, Reidel, Dordrecht, 1979, pp. 153–168.Google Scholar
Kueker, David W., Back-and-forth arguments and infinitary logics, Infinitary logic: In memoriam Carol Karp, Lecture Notes in Mathematics, vol. 492, Springer, Berlin, 1975, pp. 17–71.Google Scholar
Nadel, Mark and Stavi, Jonathan, L ∞λ-equivalence, isomorphism and potential isomorphism. Transactions of the American Mathematical Society, vol. 236 (1978), pp. 51–74.Google Scholar
Väänänen, Jouko and Veličković, Boban, Games played on partial isomorphisms. Archive for Mathematical Logic, vol. 43 (2004), no. 1, pp. 19–30.CrossRefGoogle Scholar
Väänänen, Jouko, Models and games, Cambridge Studies in Advanced Mathematics, vol. 132, Cambridge University Press, Cambridge, 2011.Google Scholar
Velleman, Dan, Simplified morasses, this Journal, vol. 49 (1984), no. 1, pp. 257–271.Google Scholar