Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hart, K.P.
Hrušák, M.
and
Verner, J.L.
2020.
Petr Simon (1944-2018).
Topology and its Applications,
Vol. 285,
Issue. ,
p.
107391.
Mildenberger, Heike
and
Shelah, Saharon
2020.
A version of $$\kappa $$-Miller forcing.
Archive for Mathematical Logic,
Vol. 59,
Issue. 7-8,
p.
879.
Fischer, Vera
Koelbing, Marlene
and
Wohofsky, Wolfgang
2023.
Fresh function spectra.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 9,
p.
103300.
Kurilić, Miloš
2025.
Copies of monomorphic structures.
Mathematica Slovaca,
Vol. 75,
Issue. 5,
p.
977.

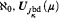 ). The “natural” means that the forcing ({
). The “natural” means that the forcing ({
