Hostname: page-component-5d84bcc8dc-qlchq Total loading time: 0 Render date: 2026-09-05T03:24:16.797Z Has data issue: false hasContentIssue false
  • English
  • Français

RANK AND RANDOMNESS

Published online by Cambridge University Press:  19 September 2019

RUPERT HÖLZL  and
CHRISTOPHER P. PORTER
RUPERT HÖLZL
Affiliation:
INSTITUT 1, FAKULTÄT FÜR INFORMATIK UNIVERSITÄT DER BUNDESWEHR MÜNCHEN WERNER-HEISENBERG-WEG 39, 85579, NEUBIBERG, GERMANY E-mail: r@hoelzl.frURL: http://hoelzl.fr
CHRISTOPHER P. PORTER
Affiliation:
DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE DRAKE UNIVERSITY DES MOINES, IA50311, USA E-mail: cp@cpporter.comURL: http://cpporter.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for each computable ordinal 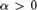$\alpha> 0$ it is possible to find in each Martin-Löf random 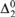${\rm{\Delta }}_2^0 $ degree a sequence R of Cantor-Bendixson rank α, while ensuring that the sequences that inductively witness R’s rank are all Martin-Löf random with respect to a single countably supported and computable measure. This is a strengthening for random degrees of a recent result of Downey, Wu, and Yang, and can be understood as a randomized version of it.

Keywords

03D3268Q30algorithmic randomnessMartin-Löf randomnessCantor-Bendixson rankcomputable measures

Information

Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 4 , December 2019 , pp. 1527 - 1543
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Ash, C. J. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, North Holland, Amsterdam, 2000.Google Scholar
Bienvenu, L. and Porter, C., Strong reductions in effective randomness. Theoretical Computer Science, vol. 459 (2012), pp. 55–68.CrossRefGoogle Scholar
Binns, S., ${\rm{\Delta }}_2^0 $ classes with complex elements , this Journal, vol. 73 (2008), no. 4, pp. 1341–1353.Google Scholar
Cenzer, D., ${\rm{\Pi }}_1^0 $classes in computability theory, Handbook of Computability Theory (Griffor, E. R., editor), Studies in Logic and the Foundations of Mathematics, vol. 140, North Holland, Amsterdam, 1999, pp. 37–85.CrossRefGoogle Scholar
Cenzer, D. and Remmel, J., Index sets for ${\rm{\Pi }}_1^0 $ classes. Annals of Pure and Applied Logic , vol. 93 (1998), no. 1–3, pp. 3–61.CrossRefGoogle Scholar
Cenzer, D. and Smith, R. L., On the ranked points of a ${\rm{\Pi }}_1^0 $ set , this Journal, vol. 54 (1989), no. 3, pp. 975–991.Google Scholar
Cholak, P. and Downey, R., On the Cantor-Bendixon rank of recursively enumerable sets, this Journal, vol. 58 (1993), no. 2, pp. 629–640.Google Scholar
Downey, R. G., Wu, G., and Yang, Y., The members of thin and minimal ${\rm{\Pi }}_1^0 $ classes, their ranks and Turing degrees. Annals of Pure and Applied Logic , vol. 166 (2015), no. 7–8, pp. 755–766.CrossRefGoogle Scholar
Hölzl, R. and Porter, C. P., Randomness for computable measures and initial segment complexity. Annals of Pure and Applied Logic, vol. 168 (2017), no. 4, pp. 860–886.CrossRefGoogle Scholar
Kautz, S. M., Degrees of random sets, Ph.D thesis, Cornell University, 1991, p. 129.Google Scholar
Kreisel, G., Analysis of the Cantor-Bendixson theorem by means of the analytic hierarchy. Bulletin de l’Académie Polonaise des Sciences, Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 7 (1959), pp. 621–626.Google Scholar
Odifreddi, P., Classical Recursion Theory Vol. II, Studies in Logic and the Foundations of Mathematics, vol. 143, North Holland, Amsterdam, 1999.Google Scholar
Owings, J., Rank, join, and Cantor singletons. Archive for Mathematical Logic, vol. 36 (1997), no. 4–5, pp. 313–320.CrossRefGoogle Scholar
Porter, C. P., Trivial measures are not so trivial. Theory of Computing Systems, vol. 56 (2015), no. 3, pp. 487–512.CrossRefGoogle Scholar
Zvonkin, A. K. and Levin, L. A., The complexity of finite objects and the basing of the concepts of information and randomness on the theory of algorithms. Uspekhi Matematicheskikh Nauk, vol. 25 (1970), no. 6(156), pp. 85–127.Google Scholar