Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lipparini, Paolo
2010.
More on regular and decomposable ultrafilters in ZFC.
Mathematical Logic Quarterly,
Vol. 56,
Issue. 4,
p.
340.
Malliaris, M.
and
Shelah, S.
2015.
Constructing regular ultrafilters from a model-theoretic point of view.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 11,
p.
8139.
Kennedy, Juliette
Shelah, Saharon
and
Väänänen, Jouko
2015.
Regular Ultrapowers at Regular Cardinals.
Notre Dame Journal of Formal Logic,
Vol. 56,
Issue. 3,
Shelah, Saharon
2021.
Atomic saturation of reduced powers.
Mathematical Logic Quarterly,
Vol. 67,
Issue. 1,
p.
18.
Sági, Gábor
2022.
Ultraproducts and Related Constructions.
Mathematics,
Vol. 11,
Issue. 1,
p.
70.


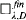 introduced in [3]. For such ultrafilters
introduced in [3]. For such ultrafilters 