Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-09T01:40:38.006Z Has data issue: false hasContentIssue false
  • English
  • Français

THE REVERSE MATHEMATICS OF THEOREMS OF JORDAN AND LEBESGUE

Part of: Computability and recursion theory General logic

Published online by Cambridge University Press:  01 February 2021

ANDRÉ NIES ,
MARCUS A. TRIPLETT  and
KEITA YOKOYAMA
ANDRÉ NIES
Affiliation:
SCHOOL OF COMPUTER SCIENCE UNIVERSITY OF AUCKLANDAUCKLAND, NEW ZEALANDE-mail: andre@cs.auckland.ac.nz
MARCUS A. TRIPLETT
Affiliation:
CENTER FOR THEORETICAL NEUROSCIENCE COLUMBIA UNIVERSITYNEW YORK, NY, USAE-mail: marcus.triplett@uq.edu.au
KEITA YOKOYAMA
Affiliation:
MATHEMATICAL INSTITUTE TOHOKU UNIVERSITYSENDAI, JAPANE-mail: keita.yokoyama.c2@tohoku.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

The Jordan decomposition theorem states that every function 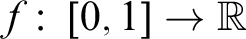$f \colon \, [0,1] \to \mathbb {R}$ of bounded variation can be written as the difference of two non-decreasing functions. Combining this fact with a result of Lebesgue, every function of bounded variation is differentiable almost everywhere in the sense of Lebesgue measure. We analyze the strength of these theorems in the setting of reverse mathematics. Over $\mathsf {RCA}_{0}$ , a stronger version of Jordan’s result where all functions are continuous is equivalent to $\mathsf {ACA}_0$ , while the version stated is equivalent to 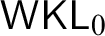${\textsf {WKL}}_{0}$ . The result that every function on 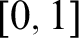$[0,1]$ of bounded variation is almost everywhere differentiable is equivalent to ${\textsf {WWKL}}_{0}$ . To state this equivalence in a meaningful way, we develop a theory of Martin–Löf randomness over $\mathsf {RCA}_0$ .

Keywords

Jordan decomposition theorembounded variationcomputable analysisreverse mathematicsrandomness

MSC classification

Primary: 03B30: Foundations of classical theories (including reverse mathematics)
Secondary: 03D78: Computation over the reals
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1657 - 1675
Check for updates
Copyright
© Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brattka, V., Miller, J. S., and Nies, A., Randomness and differentiability . Transactions of the American Mathematical Society, vol. 368 (2016), no. 1, pp. 581–605.10.1090/tran/6484CrossRefGoogle Scholar
Carothers, N., Real Analysis, Cambridge University Press, Cambridge, 2000.10.1017/CBO9780511814228CrossRefGoogle Scholar
Demuth, O., The differentiability of constructive functions of weakly bounded variation on pseudo numbers. Commentationes Mathematicae Universitatis Carolinae, vol. 16 (1975), no. 3, pp. 583–599 (Russian).Google Scholar
Downey, R., Hirschfeldt, D. R., Miller, J. S., and Nies, A., Relativizing Chaitin’s halting probability . Jounal of Mathematical Logic, vol. 5 (2005), no. 2, pp. 167–192.10.1142/S0219061305000468CrossRefGoogle Scholar
Greenberg, N., Miller, J. S., and Nies, A., Highness properties close to PA-completeness. Israel Journal of Mathematics, (2021), doi:10.1007/s11856-021-2200-7.CrossRefGoogle Scholar
Hirst, J. L., Representations of reals in reverse mathematics . Bulletin of the Polish Academy of Sciences Mathematics, vol. 55 (2007), no. 4, pp. 303–316.10.4064/ba55-4-2CrossRefGoogle Scholar
Lebesgue, H., Sur les intégrales singulières. Annales de la Faculté des sciences de Toulouse : Mathématiques (3), vol. 1 (1909), pp. 25–117.Google Scholar
Nies, A., Computability and Randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.10.1093/acprof:oso/9780199230761.001.0001CrossRefGoogle Scholar
Nies, A. and Shafer, P., Randomness notions and reverse mathematics , this Journal, vol. 85 (2020), no. 1, pp. 271–299.Google Scholar
Reimann, J. and Slaman, T. A., Measures and their random reals. Transactions of the American Mathematical Society, vol. 367 (2015), no. 7, pp. 5081–5097.10.1090/S0002-9947-2015-06184-4CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, New York, 1999, second ed., Perspectives in Logic, Association for Symbolic Logic, Cambridge University Press, New York, 2009.10.1007/978-3-642-59971-2CrossRefGoogle Scholar
Simpson, S. G. and Yokoyama, K., A nonstandard counterpart of WWKL . Notre Dame Journal of Formal Logic, vol. 52 (2011), no. 3, pp. 229–243.10.1215/00294527-1435429CrossRefGoogle Scholar
Simpson, S. G. and Yokoyama, K., Very weak fragments of weak König’s lemma. Technical note, available at https://arxiv.org/abs/2101.00636.Google Scholar
Yokoyama, K., Standard and Non-Standard Analysis in Second Order Arithmetic. Doctoral thesis, Tohoku University, 2007. Available as Tohoku Mathematical Publications 34, 2009.Google Scholar
Yu, X. and Simpson, S. G., Measure theory and weak König’s lemma . Archive for Mathematical Logic, vol. 30 (1990), no. 3, pp. 171–180.CrossRefGoogle Scholar
Zheng, X. and Rettinger, R., Effective Jordan decomposition . Theory of Computing Systems, vol. 38 (2005), no. 2, pp. 189–209.10.1007/s00224-004-1193-zCrossRefGoogle Scholar