Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Väänänen, Jouko
2008.
The Craig Interpolation Theorem in abstract model theory.
Synthese,
Vol. 164,
Issue. 3,
p.
401.
Motto Ros, Luca
2013.
The descriptive set-theoretical complexity of the embeddability relation on models of large size.
Annals of Pure and Applied Logic,
Vol. 164,
Issue. 12,
p.
1454.
Andretta, Alessandro
and
Motto Ros, Luca
2022.
Souslin quasi-orders and bi-embeddability of uncountable structures.
Memoirs of the American Mathematical Society,
Vol. 277,
Issue. 1365,

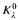 be the class of structures 〈
be the class of structures 〈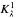 be the class of structures 〈
be the class of structures 〈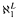 if
if 