For e.g. λ = μ+, μ regular, λ larger than the continuum, we prove a strong nonpartition result (stronger than λ → [λ; λ]2). As a consequence, the product of two topological spaces of cellularity <λ may have cellularity λ, or, in equivalent formulation, the product of two λ-c.c. Boolean algebras may lack the λ-c.c. Also λ-S-spaces and λ-L-spaces exist. In fact we deal not with successors of regular λ but with regular λ above the continuum which has a nonreflecting stationary subset of ordinals with uncountable cofinalities; sometimes we require λ to be not strong limit.

The paper is self-contained. On the nonpartition results see the closely related papers of Todorčević [T1], Shelah [Sh276] and [Sh261], and Shelah and Steprans [ShSt1].

On the cellularity of products see Todorčević [T2] and [T3], where such results were obtained for (e.g.) cf 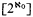and 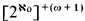; the class of cardinals he gets is quite disjoint from ours. In [Sh282] such results were obtained for more successors of singulars (mainly λ+, λ > 2cf λ). Also, concerning S and L spaces, Todorčević gets existence.

Todorčević's work on cardinals like 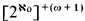relies on [Sh68] (see more in [ShA2, Chapter XIII]) (the scales appearing in the proof of 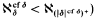). The problem was stressed in a preliminary version of the surveys of Juhasz and Monk. We give a detailed proof for one strong nonpartition theorem (1.1) and then give various strengthenings. We then use 1.10 to get the consequences (in 1.11 and 1.12).