Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
GARTI, Shimon
and
SHELAH, Saharon
2014.
Partition calculus and cardinal invariants.
Journal of the Mathematical Society of Japan,
Vol. 66,
Issue. 2,
Garti, Shimon
2017.
Amenable colorings.
European Journal of Mathematics,
Vol. 3,
Issue. 1,
p.
77.
Garti, Shimon
Magidor, Menachem
and
Shelah, Saharon
2018.
On the Spectrum of Characters of Ultrafilters.
Notre Dame Journal of Formal Logic,
Vol. 59,
Issue. 3,
Shelah, Saharon
2020.
On CON(𝔡_{𝜆}> cov_{𝜆}(meagre)).
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 8,
p.
5351.
Garti, Shimon
2021.
Unbalanced polarized relations.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 3,
p.
1281.
Honzik, Radek
and
Stejskalová, Šárka
2022.
Small $$\mathfrak {u}(\kappa )$$ at singular $$\kappa $$ with compactness at $$\kappa ^{++}$$.
Archive for Mathematical Logic,
Vol. 61,
Issue. 1-2,
p.
33.
Lambie-Hanson, Chris
2023.
A Galvin–Hajnal theorem for generalized cardinal characteristics.
European Journal of Mathematics,
Vol. 9,
Issue. 1,
Benhamou, T.
and
Jirattikansakul, S.
2023.
A small ultrafilter number at every singular cardinal.
Acta Mathematica Hungarica,
Vol. 171,
Issue. 1,
p.
12.
Shelah, Saharon
2023.
Corrected iteration.
Bollettino dell'Unione Matematica Italiana,
Vol. 16,
Issue. 3,
p.
521.
Inamdar, Tanmay
and
Rinot, Assaf
2024.
Was Ulam right? II: small width and general ideals.
Algebra universalis,
Vol. 85,
Issue. 2,
Shelah, Saharon
2025.
Twins: non-isomorphic models forced to be isomorphic Part I.
Monatshefte für Mathematik,

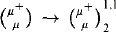 is consistent with ZFC, for a singular
is consistent with ZFC, for a singular 