Published online by Cambridge University Press: 23 October 2018
We investigate which filters on ω can contain towers, that is, a modulo finite descending sequence without any pseudointersection (in 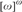 ${[\omega ]^\omega }$). We prove the following results:
${[\omega ]^\omega }$). We prove the following results:
(1) Many classical examples of nice tall filters contain no towers (in ZFC).
(2) It is consistent that tall analytic P-filters contain towers of arbitrary regular height (simultaneously for many regular cardinals as well).
(3) It is consistent that all towers generate nonmeager filters (this answers a question of P. Borodulin-Nadzieja and D. Chodounský), in particular (consistently) Borel filters do not contain towers.
(4) The statement “Every ultrafilter contains towers.” is independent of ZFC (this improves an older result of K. Kunen, J. van Mill, and C. F. Mills).
Furthermore, we study many possible logical (non)implications between the existence of towers in filters, inequalities between cardinal invariants of filters (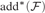 ${\rm{ad}}{{\rm{d}}^{\rm{*}}}\left( {\cal F} \right)$,
${\rm{ad}}{{\rm{d}}^{\rm{*}}}\left( {\cal F} \right)$, 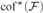 ${\rm{co}}{{\rm{f}}^{\rm{*}}}\left( {\cal F} \right)$,
${\rm{co}}{{\rm{f}}^{\rm{*}}}\left( {\cal F} \right)$, 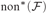 ${\rm{no}}{{\rm{n}}^{\rm{*}}}\left( {\cal F} \right)$, and
${\rm{no}}{{\rm{n}}^{\rm{*}}}\left( {\cal F} \right)$, and 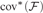 ${\rm{co}}{{\rm{v}}^{\rm{*}}}\left( {\cal F} \right)$), and the existence of Luzin type families (of size
${\rm{co}}{{\rm{v}}^{\rm{*}}}\left( {\cal F} \right)$), and the existence of Luzin type families (of size 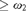 $\ge {\omega _2}$), that is, if
$\ge {\omega _2}$), that is, if 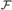 ${\cal F}$ is a filter then
${\cal F}$ is a filter then 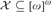 ${\cal X} \subseteq {[\omega ]^\omega }$ is an
${\cal X} \subseteq {[\omega ]^\omega }$ is an 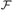 ${\cal F}$-Luzin family if
${\cal F}$-Luzin family if 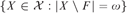 $\left\{ {X \in {\cal X}:|X \setminus F| = \omega } \right\}$ is countable for every
$\left\{ {X \in {\cal X}:|X \setminus F| = \omega } \right\}$ is countable for every 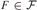 $F \in {\cal F}$.
$F \in {\cal F}$.