Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mildenberger, Heike
and
Shelah, Saharon
2000.
Changing cardinal characteristics without changing ω-sequences or cofinalities.
Annals of Pure and Applied Logic,
Vol. 106,
Issue. 1-3,
p.
207.
Džamonja, Mirna
and
Shelah, Saharon
2004.
On the existence of universal models.
Archive for Mathematical Logic,
Vol. 43,
Issue. 7,
p.
901.
Rosłanowski, Andrzej
and
Shelah, Saharon
2008.
Generating ultrafilters in a reasonable way.
Mathematical Logic Quarterly,
Vol. 54,
Issue. 2,
p.
202.
Shelah, Saharon
2012.
Many partition relations below density.
Israel Journal of Mathematics,
Vol. 191,
Issue. 2,
p.
507.
Shelah, Saharon
2017.
Logic Colloquium '01.
p.
402.
Raghavan, Dilip
and
Todorcevic, Stevo
2020.
Proof of a conjecture of Galvin.
Forum of Mathematics, Pi,
Vol. 8,
Issue. ,
Shelah, Saharon
2020.
On CON(𝔡_{𝜆}> cov_{𝜆}(meagre)).
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 8,
p.
5351.
CHEN-MERTENS, WILLIAM
KOJMAN, MENACHEM
and
STEPRĀNS, JURIS
2021.
STRONG COLORINGS OVER PARTITIONS.
The Bulletin of Symbolic Logic,
Vol. 27,
Issue. 1,
p.
67.
Shelah, Saharon
2022.
Forcing axioms for λ‐complete μ+$\mu ^+$‐c.c. .
Mathematical Logic Quarterly,
Vol. 68,
Issue. 1,
p.
6.

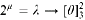 and even
and even 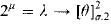 for
for 