No CrossRef data available.
Article contents
WEAKLY 2-RANDOMS AND 1-GENERICS IN SCOTT SETS
Published online by Cambridge University Press: 01 May 2018
Abstract
Let 
${\cal S}$ be a Scott set, or even an ω-model of WWKL. Then for each A ε S, either there is X ε S that is weakly 2-random relative to A, or there is X ε S that is 1-generic relative to A. It follows that if A1,…,An ε S are noncomputable, there is X ε S such that each Ai is Turing incomparable with X, answering a question of Kučera and Slaman. More generally, any ∀∃ sentence in the language of partial orders that holds in 
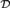${\cal D}$ also holds in 
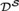${{\cal D}^{\cal S}}$, where 
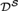${{\cal D}^{\cal S}}$ is the partial order of Turing degrees of elements of 
${\cal S}$.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
Conidis, C. J., A measure-theoretic proof of Turing incomparability. Annals of Pure and Applied Logic, vol. 162 (2010), no. 1, pp. 83–88.CrossRefGoogle Scholar
>Downey, R., Nies, A., Weber, R., and Yu, L., Lowness and 
${\rm{\Pi }}_2^0$ nullsets, this Journal, vol. 71 (2006), no. 3, pp. 1044–1052.Downey,+R.,+Nies,+A.,+Weber,+R.,+and+Yu,+L.,+Lowness+and+${\rm{\Pi+}}_2^0$+nullsets,+this+Journal,+vol.+71+(2006),+no.+3,+pp.+1044–1052.>Google Scholar
${\rm{\Pi }}_2^0$ nullsets, this Journal, vol. 71 (2006), no. 3, pp. 1044–1052.Downey,+R.,+Nies,+A.,+Weber,+R.,+and+Yu,+L.,+Lowness+and+${\rm{\Pi+}}_2^0$+nullsets,+this+Journal,+vol.+71+(2006),+no.+3,+pp.+1044–1052.>Google ScholarKučera, A. and Slaman, T. A., Turing incomparability in Scott sets. Proceedings of the American Mathematical Society, vol. 135 (2007), no. 11, pp. 3723–3731.CrossRefGoogle Scholar
>Lerman, M., Degrees of Unsolvability, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1983.Google Scholar
>Li, W. and Slaman, T. A., Private communication.Li,+W.+and+Slaman,+T.+A.,+Private+communication.>Google Scholar
>Nies, A., Computability and Randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.CrossRefGoogle Scholar