Article contents
AN EXISTENTIAL ∅-DEFINITION OF 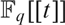 $F_q [[t]]$ IN
$F_q [[t]]$ IN 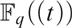 $F_q \left( t \right)$
$F_q \left( t \right)$
Published online by Cambridge University Press: 12 December 2014
Abstract
We show that the valuation ring 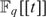 $F_q [[t]]$ in the local field
$F_q [[t]]$ in the local field 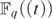 $F_q \left( t \right)$ is existentially definable in the language of rings with no parameters. The method is to use the definition of the henselian topology following the work of Prestel-Ziegler to give an ∃-
$F_q \left( t \right)$ is existentially definable in the language of rings with no parameters. The method is to use the definition of the henselian topology following the work of Prestel-Ziegler to give an ∃-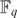 $F_q $-definable bounded neighbouhood of 0. Then we “tweak” this set by subtracting, taking roots, and applying Hensel’s Lemma in order to find an ∃-
$F_q $-definable bounded neighbouhood of 0. Then we “tweak” this set by subtracting, taking roots, and applying Hensel’s Lemma in order to find an ∃-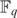 $F_q $-definable subset of
$F_q $-definable subset of 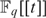 $F_q [[t]]$ which contains
$F_q [[t]]$ which contains 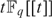 $tF_q [[t]]$. Finally, we use the fact that
$tF_q [[t]]$. Finally, we use the fact that 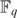 $F_q $ is defined by the formula
$F_q $ is defined by the formula 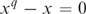 $x^q- x = 0$ to extend the definition to the whole of
$x^q- x = 0$ to extend the definition to the whole of 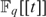 $F_q [[t]]$ and to rid the definition of parameters.
$F_q [[t]]$ and to rid the definition of parameters.
Several extensions of the theorem are obtained, notably an ∃-∅-definition of the valuation ring of a nontrivial valuation with divisible value group.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2014
References
REFERENCES
- 8
- Cited by

