Article contents
An introduction to forking
Published online by Cambridge University Press: 12 March 2014
Extract
The notion of forking has been introduced by Shelah, and a full treatment of it will appear in his book on stability [S1]. The principal aim of this paper is to show that it is an easy and natural notion.
Consider some well-known examples of ℵ0-stable theories: vector spaces over Q, algebraically closed fields, differentially closed fields of characteristic 0; in each of these cases, we have a natural notion of independence: linear, algebraic and differential independence respectively. Forking gives a generalization of these notions. More precisely, if 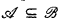 are subsets of some model
are subsets of some model 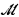 and c a point of this model, the fact that the type of c over
and c a point of this model, the fact that the type of c over 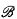 does not fork over
does not fork over 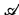 means that there are no more relations of dependence between c and
means that there are no more relations of dependence between c and 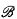 than there already existed between c and
than there already existed between c and 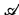 . In the case of the vector spaces, this means that c is in the space generated by
. In the case of the vector spaces, this means that c is in the space generated by 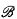 only if it is already in the space generated by
only if it is already in the space generated by 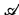 . In the case of differentially closed fields, this means that the minimal differential equations of c with coefficient respectively in
. In the case of differentially closed fields, this means that the minimal differential equations of c with coefficient respectively in 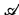 and
and 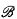 have the same order. Of course, these notions of dependence are essential for the study of the above mentioned structures. Forking is no less important for stable theories. A glance at Shelah's book will convince the reader that this is the case.
have the same order. Of course, these notions of dependence are essential for the study of the above mentioned structures. Forking is no less important for stable theories. A glance at Shelah's book will convince the reader that this is the case.
What we have to do is the following. Assuming T stable and given 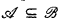 and p a type on
and p a type on 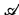 , we want to distinguish among the extensions of p to
, we want to distinguish among the extensions of p to 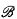 some ofthem that we shall call the nonforking extensions of p.
some ofthem that we shall call the nonforking extensions of p.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1979
References
REFERENCES
- 60
- Cited by

