Article contents
Analytic equivalence relations and bi-embeddability
Published online by Cambridge University Press: 12 March 2014
Abstract
Louveau and Rosendal [5] have shown that the relation of bi-embeddability for countable graphs as well as for many other natural classes of countable structures is complete under Borel reducibility for analytic equivalence relations. This is in strong contrast to the case of the isomorphism relation, which as an equivalence relation on graphs (or on any class of countable structures consisting of the models of a sentence of 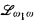 ) is far from complete (see [5, 2]).
) is far from complete (see [5, 2]).
In this article we strengthen the results of [5] by showing that not only does bi-embeddability give rise to analytic equivalence relations which are complete under Borel reducibility, but in fact any analytic equivalence relation is Borel equivalent to such a relation. This result and the techniques introduced answer questions raised in [5] about the comparison between isomorphism and bi-embeddability. Finally, as in [5] our results apply not only to classes of countable structures defined by sentences of 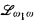 , but also to discrete metric or ultrametric Polish spaces, compact metrizable topological spaces and separable Banach spaces, with various notions of embeddability appropriate for these classes, as well as to actions of Polish monoids.
, but also to discrete metric or ultrametric Polish spaces, compact metrizable topological spaces and separable Banach spaces, with various notions of embeddability appropriate for these classes, as well as to actions of Polish monoids.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2011
References
REFERENCES
- 12
- Cited by

