Online ordering is currently unavailable due to technical issues. We apologise for any delays responding to customers while we resolve this. For further updates please visit our website: https://www.cambridge.org/news-and-insights/technical-incident Due to planned maintenance there will be periods of time where the website may be unavailable. We apologise for any inconvenience.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 12 March 2014
Since 1934 various different techniques for natural deduction have been developed by Gentzen, Jaśkowski, Rosser, Quine, and others (see [1], pp. 147–167; [2], especially footnotes 1, 3, and 4; and [3], pp. 75-83, 96-107, and 289-294). It has been pointed out to me by Professor Donald Kalish of U.C.L.A. that the restrictions placed upon Universal Generalization (UG) and Existential Instantiation (EI) in [3] force one to construct a less natural proof than seems desirable for such arguments as
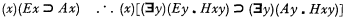
(cf. [3], p. 139, and [1], pp. 175f.) It is my purpose in this note to formulate an alternative restriction on UG which will permit a more natural proof for such arguments, and to prove the consistency of the altered rule.
In the notation of [3], “The expression ‘Φμ’ will denote any propositional function in which there is at least one free occurrence of the variable denoted by ‘μ’. The expression ‘Φν’ will denote the result of replacing all free occurrences of μ in Φμ by ν, with the added proviso that when ν is a variable it must occur free in Φν at all places at which μ occurs free in Φμ.” ([3], p. 100.) The statement of EI is relatively unrestricted; being
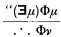
provided that ν is a variable which occurs free in no earlier step.” ([3], p. 104.)
