Article contents
AXIOM I0 AND HIGHER DEGREE THEORY
Published online by Cambridge University Press: 22 July 2015
Abstract
In this paper, we analyze structures of Zermelo degrees via a list of four degree theoretic questions (see §2) in various fine structure extender models, or under large cardinal assumptions. In particular we give a detailed analysis of the structures of Zermelo degrees in the Mitchell model for ω many measurable cardinals. It turns out that there is a profound correlation between the complexity of the degree structures at countable cofinality singular cardinals and the large cardinal strength of the relevant cardinals. The analysis applies to general degree notions, Zermelo degree is merely the author’s choice for illustrating the idea.
I0(λ) is the assertion that there is an elementary embedding j : L(Vλ+1) → L(Vλ+1) with critical point < λ. We show that under I0(λ), the structure of Zermelo degrees at λ is very complicated: it has incomparable degrees, is not dense, satisfies Posner–Robinson theorem etc. In addition, we show that I0 together with a mild condition on the critical point of the embedding implies that the degree determinacy for Zermelo degrees at λ is false in L(Vλ+1). The key tool in this paper is a generic absoluteness theorem in the theory of I0, from which we obtain an analogue of Perfect Set Theorem for “projective” subsets of Vλ+1, and the Posner–Robinson follows as a corollary. Perfect Set Theorem and Posner–Robinson provide evidences supporting the analogy between 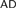 $$AD$$ over L(ℝ) and I0 over L(Vλ+1), while the failure of degree determinacy is one for disanalogy. Furthermore, we conjecture that the failure of degree determinacy for Zermelo degrees at any uncountable cardinal is a theorem of
$$AD$$ over L(ℝ) and I0 over L(Vλ+1), while the failure of degree determinacy is one for disanalogy. Furthermore, we conjecture that the failure of degree determinacy for Zermelo degrees at any uncountable cardinal is a theorem of 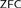 $$ZFC$$.
$$ZFC$$.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2015
References
REFERENCES
- 6
- Cited by

