Article contents
BINARY PRIMITIVE HOMOGENEOUS SIMPLE STRUCTURES
Published online by Cambridge University Press: 21 March 2017
Abstract
Suppose that 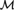 ${\cal M}$ is countable, binary, primitive, homogeneous, and simple. We prove that the SU-rank of the complete theory of
${\cal M}$ is countable, binary, primitive, homogeneous, and simple. We prove that the SU-rank of the complete theory of 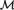 ${\cal M}$ is 1 and hence 1-based. It follows that
${\cal M}$ is 1 and hence 1-based. It follows that 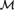 ${\cal M}$ is a random structure. The conclusion that
${\cal M}$ is a random structure. The conclusion that 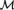 ${\cal M}$ is a random structure does not hold if the binarity condition is removed, as witnessed by the generic tetrahedron-free 3-hypergraph. However, to show that the generic tetrahedron-free 3-hypergraph is 1-based requires some work (it is known that it has the other properties) since this notion is defined in terms of imaginary elements. This is partly why we also characterize equivalence relations which are definable without parameters in the context of ω-categorical structures with degenerate algebraic closure. Another reason is that such characterizations may be useful in future research about simple (nonbinary) homogeneous structures.
${\cal M}$ is a random structure does not hold if the binarity condition is removed, as witnessed by the generic tetrahedron-free 3-hypergraph. However, to show that the generic tetrahedron-free 3-hypergraph is 1-based requires some work (it is known that it has the other properties) since this notion is defined in terms of imaginary elements. This is partly why we also characterize equivalence relations which are definable without parameters in the context of ω-categorical structures with degenerate algebraic closure. Another reason is that such characterizations may be useful in future research about simple (nonbinary) homogeneous structures.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 1
- Cited by

