Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-23T05:29:06.961Z Has data issue: false hasContentIssue false
  • English
  • Français

Boolean algebras, Stone spaces, and the iterated Turing jump

Published online by Cambridge University Press:  12 March 2014

Carl G. Jockusch Jr.  and
Robert I. Soare
Carl G. Jockusch Jr.
Affiliation:
Department of Mathematics, University of Illinois, Urbana, Illinois 61801, E-mail: jockusch@math.uiuc.edu
Robert I. Soare
Affiliation:
Department of Mathematics, University of Chicago, Chicago, Illinois 60637, E-mail: soare@math.uchicago.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We show, roughly speaking, that it requires ω iterations of the Turing jump to decode nontrivial information from Boolean algebras in an isomorphism invariant fashion. More precisely, if α is a recursive ordinal, 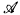is a countable structure with finite signature, and d is a degree, we say that 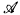has αth-jump degreed if d is the least degree which is the αth jump of some degree c such there is an isomorphic copy of 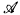with universe ω in which the functions and relations have degree at most c. We show that every degree d ≥ 0(ω) is the ωth jump degree of a Boolean algebra, but that for n < ω no Boolean algebra has nth-jump degree d < 0(n). The former result follows easily from work of L. Feiner. The proof of the latter result uses the forcing methods of J. Knight together with an analysis of various equivalences between Boolean algebras based on a study of their Stone spaces. A byproduct of the proof is a method for constructing Stone spaces with various prescribed properties.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 4 , December 1994 , pp. 1121 - 1138
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ash, C. J., Jockusch, C. G., and Knight, J. F., Jumps of orderings, Transactions of the American Mathematical Society, vol. 319 (1990), pp. 573–599.CrossRefGoogle Scholar
[2]Downey, R. and Jockusch, C. G., Every low Boolean algebra is isomorphic to a recursive one, Proceeding of the American Mathematical Society (to appear).Google Scholar
[3]Downey, R. and Knight, J. F., Orderings with αth-jump degree 0(α), Proceedings of the American Mathematical Society, vol. 114 (1992), pp. 545–552.Google Scholar
[4]Epstein, R., Degrees of unsolvability: Structure and theory, Lecture Notes in Mathematics, vol. 759, Springer-Verlag, Berlin, Heidelberg, and New York, 1979.Google Scholar
[5]Feiner, L., Hierarchies of Boolean algebras, this Journal, vol. 35 (1970), pp. 365–374.Google Scholar
[6]Jockusch, C. G. and Soare, R. I., Degrees of orderings not isomorphic to recursive linear orderings, Annals of Pure and Applied Logic, vol. 52 (1991), pp. 39–64.CrossRefGoogle Scholar
[7]Kelley, J. L., General Topology, D. Van Nostrand Company, Princeton, Toronto, New York, and London, 1955.Google Scholar
[8]Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), pp. 1034–1042.Google Scholar
[9]Koppelberg, S., Boolean algebras and Boolean spaces, Handbook of Boolean algebras (Monk, J., editor), vol. 1, North-Holland, Amsterdam, New York, Oxford, and Tokyo, 1989, pp. 95–106.Google Scholar
[10]Läuchli, H., A decision procedure for the weak second order theory of linear order, Contributions to mathematical logic, Colloquium, Hannover, 1966, North-Holland, Amsterdam, 1968, pp. 189–197.Google Scholar
[11]Macintyre, J., Transfinite extensions of Friedberg's completeness criterion, this Journal, vol. 42 1977), pp. 1–10.Google Scholar
[12]Rabin, M. O., Decidability of second-order theories and automata on infinite trees, Transactions if the American Mathematical Society, vol. 141 (1969), pp. 1–35.Google Scholar
[13]Rabin, M. O., Automata on infinite objects and Church's problem, Regional Conference Series in Mathematics, Number 13, American Mathematical Society, Providence, Rhode Island, 1972.Google Scholar
[14]Remmel, J., Recursive Boolean algebras, Handbook of Boolean Algebras (Monk, J., editor), vol. 3, North-Holland, Amsterdam, New York, Oxford, and Tokyo, 1989, pp. 1097–1165.Google Scholar
[15]Richter, L. J., Degrees of unsolvability of models, Ph.D. thesis, University of Illinois Urbana-Champaign, Urbana, Illinois, 1977.Google Scholar
[16]Richter, L. J., Degrees of structures, this Journal, vol. 46 (1981), pp. 723–731.Google Scholar
[17]Rosenstein, J., Linear orderings, Academic Press, New York, 1982.Google Scholar
[18]Thurber, J., Every low2Boolean algebra has a recursive copy (to appear).Google Scholar