Article contents
Boolean extensions which efface the Mahlo property1
Published online by Cambridge University Press: 12 March 2014
Extract
The results that follow are intended to be understood as informal counterparts to formal theorems of Zermelo-Fraenkel set theory with choice. Basic notation not explained here can usually be found in [5]. It will also be necessary to assume a knowledge of the fundamentals of boolean and generic extensions, in the style of Jech's monograph [3]. Consistency results will be stated as assertions about the existence of certain complete boolean algebras, B, C , etc., either outright or in the sense of a countable standard transitive model M of ZFC augmented by hypotheses about the existence of various large cardinals. Proofs will usually be phrased in terms of the forcing relation ⊩ over such an M, especially when they make heavy use of genericity. They are then assertions about Shoenfield-style P -generic extensions M(G), in which the ‘names’ are required without loss of generality to be elements of M B = (V B )M, B is the boolean completion of P in M (cf. [3, p. 50]: the notation there is RO(P)), the generic G is named by Ĝ ∈ M B such that (⟦p ∈ Ĝ⟧ B = p and 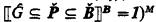 (cf. [11, p. 361] and [3, pp. 58–59]), and for p ∈ P and c 1, …, cn ∈ M B , p ⊩ φ(c 1, …, cn ) iff ⟦φ(c 1, …, cn )⟧B ≥ p (cf. [3, pp. 61–62]).
(cf. [11, p. 361] and [3, pp. 58–59]), and for p ∈ P and c 1, …, cn ∈ M B , p ⊩ φ(c 1, …, cn ) iff ⟦φ(c 1, …, cn )⟧B ≥ p (cf. [3, pp. 61–62]).
Some prior acquaintance with large cardinal theory is also needed. At this writing no comprehensive introductory survey is yet in print, though [1], [10], [12]and [13] provide partial coverage. The scheme of definitions which follows is intended to fix notation and serve as a glossary for reference, and it is followed in turn by a description of the results of the paper. We adopt the convention that κ, λ, μ, ν, ρ and σ vary over infinite cardinals, and all other lower case Greek letters (except χ, φ, ψ, ϵ) over arbitrary ordinals.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
Footnotes
This paper is a revision of the first half of the author's Ph.D. thesis, written under the supervision of Professor Kenneth Kunen, and submitted to the University of Wisconsin in August, 1971. I would like to thank Professor Kunen for his persistent encouragement and quietly infallible guidance in teaching me set theory. I would also like to thank Professor Karel Prikry for introducing me to techniques of Jensen and Mitchell that are basic to the results of this paper.
References
REFERENCES
- 5
- Cited by

