Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Affatato, Maria L.
Kent, Thomas F.
and
Sorbi, Andrea
2008.
Branching in the $${\Sigma^0_2}$$ -enumeration degrees: a new perspective.
Archive for Mathematical Logic,
Vol. 47,
Issue. 3,
p.
221.
Badillo, Liliana
Bianchini, Caterina
Ganchev, Hristo
Kent, Thomas F.
and
Sorbi, Andrea
2016.
A note on the enumeration degrees of 1-generic sets.
Archive for Mathematical Logic,
Vol. 55,
Issue. 3-4,
p.
405.
Badillo, Liliana
Harris, Charles M.
and
Soskova, Mariya I.
2018.
Enumeration 1-Genericity in the Local Enumeration Degrees.
Notre Dame Journal of Formal Logic,
Vol. 59,
Issue. 4,
Ganchev, Hristo
and
Sariev, Andrey C.
2021.
The automorphism group and definability of the jump operator in the $$\omega $$-enumeration degrees.
Archive for Mathematical Logic,
Vol. 60,
Issue. 7-8,
p.
909.

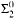 enumeration degree bounds a nonsplitting nonzero enumeration degree.
enumeration degree bounds a nonsplitting nonzero enumeration degree.