Published online by Cambridge University Press: 12 March 2014
Our main results are:
Theorem 1. Con(ZFC + “every function f: ω1 → ω1 is dominated by a canonical function”) implies Con(ZFC + “there exists an inaccessible limit of measurable cardinals”). [In fact equiconsistency holds.]
Theorem 3. Con(ZFC + “there exists a non-regular uniform ultrafilter on ω1”) implies Con(ZFC + “there exists an inaccessible stationary limit of measurable cardinals”).
Theorem 5. Con (ZFC + “there exists an ω1-sequence 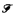 of ω1-complete uniform filters on ω1 s.t. every A ⊆ ω1 is measurable w.r.t. a filter in
of ω1-complete uniform filters on ω1 s.t. every A ⊆ ω1 is measurable w.r.t. a filter in 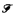 (Ulam property)”) implies Con(ZFC + “there exists an inaccessible stationary limit of measurable cardinals”).
(Ulam property)”) implies Con(ZFC + “there exists an inaccessible stationary limit of measurable cardinals”).
We start with a discussion of the canonical functions and look at some combinatorial principles. Assuming the domination property of Theorem 1, we use the Ketonen diagram to show that ω2V is a limit of measurable cardinals in Jensen's core model KMO for measures of order zero. Using related arguments we show that ω2V is a stationary limit of measurable cardinals in KMO, if there exists a weakly normal ultrafilter on ω1. The proof yields some other results, e.g., on the consistency strength of weak*-saturated filters on ω1, which are of interest in view of the classical Ulam problem.