Hostname: page-component-cb9f654ff-rkzlw Total loading time: 0 Render date: 2025-08-11T19:31:39.027Z Has data issue: false hasContentIssue false
  • English
  • Français

CLASSIFYING SPACES AND THE LASCAR GROUP

Part of: Applied homological algebra and category theory Model theory

Published online by Cambridge University Press:  13 September 2021

TIM CAMPION ,
GREG COUSINS  and
JINHE YE Open the ORCID record for JINHE YE [Opens in a new window]
TIM CAMPION
Affiliation:
DEPARTMENT OF MATHEMATICS JOHNS HOPKINS UNIVERSITY BALTIMORE, MD, USA E-mail: tcampio1@jh.edu
GREG COUSINS
Affiliation:
DEPARTMENT OF MATHEMATICS & STATISTICS McMASTER UNIVERSITY HAMILTON, ON, CANADA E-mail: cousingd@mcmaster.ca
JINHE YE
Affiliation:
INSTITUT DE MATHÉMATIQUES DE JUSSIEU—PARIS RIVE GAUCHE SORBONNE UNIVERSITÉ PARIS, FRANCE E-mail: jinhe.ye@imj-prg.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the Lascar group 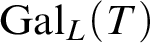$\operatorname {Gal}_L(T)$ of a first-order theory T is naturally isomorphic to the fundamental group 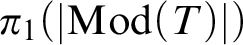$\pi _1(|\mathrm {Mod}(T)|)$ of the classifying space of the category of models of T and elementary embeddings. We use this identification to compute the Lascar groups of several example theories via homotopy-theoretic methods, and in fact completely characterize the homotopy type of 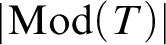$|\mathrm {Mod}(T)|$ for these theories T. It turns out that in each of these cases, 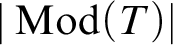$|\operatorname {Mod}(T)|$ is aspherical, i.e., its higher homotopy groups vanish. This raises the question of which homotopy types are of the form 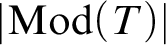$|\mathrm {Mod}(T)|$ in general. As a preliminary step towards answering this question, we show that every homotopy type is of the form 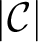$|\mathcal {C}|$ where 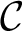$\mathcal {C}$ is an Abstract Elementary Class with amalgamation for 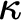$\kappa $-small objects, where 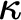$\kappa $ may be taken arbitrarily large. This result is improved in another paper.

Keywords

classifying spaceLascar grouphomotopy type

MSC classification

Primary: 03C48: Abstract elementary classes and related topics
Secondary: 03C52: Properties of classes of models 55U10: Simplicial sets and complexes

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1396 - 1431
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adámek, J. and Rosický, J., Locally Presentable and Accessible Categories, Cambridge University Press, Cambridge, 1994.10.1017/CBO9780511600579CrossRefGoogle Scholar
Antolín-Camarena, O., Lots of categories are contractible, unpublished expository note. Available at https://www.matem.unam.mx/~omar/notes/contractible.html (accessed 08 March 2018).Google Scholar
Barnea, I. and Schlank, T. M., Model structures on IND-categories and the accessibility rank of weak equivalences. Homology, Homotopy and Applications, vol. 17 (2015), no. 2, pp. 235–260.10.4310/HHA.2015.v17.n2.a12CrossRefGoogle Scholar
Beke, T. and Rosický, J., Abstract elementary classes and accessible categories. Annals of Pure and Applied Logic, vol. 163 (2012), no. 12, pp. 2008–2017.10.1016/j.apal.2012.06.003CrossRefGoogle Scholar
Campion, T. and Ye, J., Homotopy types of abstract elementary classes. Journal of Pure and Applied Algebra, vol. 225 (2021), no. 5, p. 106461.CrossRefGoogle Scholar
Casanovas, E. and Peláez, R., ${\left|t\right|}^{+}$ -resplendent models and the lascar group. Mathematical Logic Quarterly, vol. 51 (2005), no. 6, pp. 626–631.10.1002/malq.200510012CrossRefGoogle Scholar
Casanovas, E. et al., Galois groups of first order theories. Journal of Mathematical Logic, vol. 1 (2001), no. 02, pp. 305–319.CrossRefGoogle Scholar
Chang, C. C. and Keisler, H. J., Model Theory, third ed., Studies in Logic and the Foundations of Mathematics, vol. 73, North-Holland Publishing Co., Amsterdam, 1990.Google Scholar
Dobrowolski, J., Kim, B., and Lee, J., The Lascar groups and the first homology groups in model theory. Annals of Pure and Applied Logic, vol. 168 (2017), no. 12, pp. 2129–2151.10.1016/j.apal.2017.06.006CrossRefGoogle Scholar
Dwyer, W. and Kan, D., Calculating simplicial localizations. Journal of Pure and Applied Algebra, vol. 18 (1980), no. 1, pp. 17–35.CrossRefGoogle Scholar
Gabriel, P. and Zisman, M., Calculus of Fractions and Homotopy Theory, Springer-Verlag, New York, 1967.10.1007/978-3-642-85844-4CrossRefGoogle Scholar
Goerss, P. and Jardine, J. F., Simplicial Homotopy Theory, Birkhäuser Verlag, Basel, 2009.10.1007/978-3-0346-0189-4CrossRefGoogle Scholar
Goodrick, J., Kim, B., and Kolesnikov, A., Homology groups of types in model theory and the computation of ${H}_2(p)$ , this Journal, vol. 78 (2013), no. 4, pp. 1086–1114.Google Scholar
Hatcher, A., Algebraic Topology, Cambridge University Press, 2002.Google Scholar
Hrushovski, E., Definability patterns and their symmetries, preprint, 2019, arXiv:1911.01129.Google Scholar
Kan, D. M., On c.s.s. complexes. American Journal of Mathematics, vol. 79 (1957), pp. 449–476.10.2307/2372558CrossRefGoogle Scholar
Kaplansky, I., Maximal fields with valuations. Duke Mathematical Journal, vol. 9 (1942), no. 2, pp. 303–321.10.1215/S0012-7094-42-00922-0CrossRefGoogle Scholar
Kruckman, A., If has amalgamation, does have amalgamation? MathOverflow, version: 2018-06-29. Available at https://mathoverflow.net/q/303884.Google Scholar
Lane, S. M., Categories for the Working Mathematician, Springer-Verlag, New York, 1998.Google Scholar
Lascar, D., On the category of models of a complete theory, this Journal, vol. 47 (1982), no. 2, pp. 249–266.Google Scholar
Lieberman, M. and Rosický, J., Classification theory for accessible categories, this Journal, vol. 81 (2016), no. 1, pp. 151–165.Google Scholar
Low, Z. L., Does ${\mathsf{Ind}}_{\unicode{x3bb}}^{\unicode{x3bc}}({\mathsf{Ind}}_{\unicode{x3ba}}^{\unicode{x3bb}}(\rfloor))= {\mathsf{Ind}}_{\unicode{x3ba}}^{\unicode{x3bc}}(\rfloor)?$ MathOverflow. Available at https://mathoverflow.net/q/382273.Google Scholar
Low, Z. L., The heart of a combinatorial model category. Theory and Applications of Categories, vol. 31 (2016), pp. 31–62.Google Scholar
May, J. P., The dual whitehead theorems. London Mathematical Society Lecture Note Series, vol. 86 (1983), pp. 46–54.Google Scholar
May, J. P., Simplicial Objects in Algebraic Topology, University of Chicago Press, Chicago, 1992.Google Scholar
Milnor, J., The geometric realization of a semi-simplicial complex. Annals of Mathematics. Second Series, vol. 65 (1957), pp. 357–362.10.2307/1969967CrossRefGoogle Scholar
Paré, R., Simply connected limits. Canadian Journal of Mathematics, vol. 42 (1990), no. 4, pp. 731–746.10.4153/CJM-1990-038-6CrossRefGoogle Scholar
Poonen, B., Maximally complete fields. L'Enseignement Mathématique, vol. 39 (1993), nos. 1–2, pp. 87–106.Google Scholar
Quillen, D. G., Homotopical Algebra, Springer-Verlag, Berlin, 1967.10.1007/BFb0097438CrossRefGoogle Scholar
Quillen, D., Higher algebraic K-theory: I, Higher K-Theories (Bass, H., editor), Springer, Berlin, 1973, pp. 85–147.10.1007/BFb0067053CrossRefGoogle Scholar
Raptis, G. and Rosický, J., The accessibility rank of weak equivalences. Theory and Applications of Categories, vol. 30 (2015, pp. 687–703.Google Scholar
Riehl, E., A leisurely introduction to simplicial sets, unpublished expository note. Available at http://www.math.jhu.edu/~eriehl/ssets.pdf (accessed 06 July 2018).Google Scholar
Riehl, E., Category Theory in Context, Courier Dover Publications, Mineola, NY, 2017.Google Scholar
Schapira, P. and Kashiwara, M., Categories and Sheaves, Grundlehren der Mathematischen Wissenschaften, vol. 332, Springer-Verlag, Berlin, 2006.Google Scholar
Shelah, S., Classification Theory for Abstract Elementary Classes, College Publications, London, 2009.Google Scholar
Simon, P., A Guide to NIP Theories, Lecture Notes in Logic, vol. 44, Cambridge University Press, Cambridge, 2015.CrossRefGoogle Scholar
Steenrod, N. E. et al., A convenient category of topological spaces. The Michigan Mathematical Journal, vol. 14 (1967), no. 2, pp. 133–152.10.1307/mmj/1028999711CrossRefGoogle Scholar
Tent, K. and Ziegler, M., A Course in Model Theory, Lecture Notes in Logic, vol. 40, Cambridge University Press, Cambridge, 2012.CrossRefGoogle Scholar
Thomason, R. W., Cat as a closed model category. Cahiers de Topologie et Géométrie Différentielle Catégoriques, vol. 21 (1980), no. 3, pp. 305–324.Google Scholar
Ward Henson, C., A family of countable homogeneous graphs. Pacific Journal of Mathematics, vol. 38 (1971), pp. 69–83.CrossRefGoogle Scholar
van den Dries, L., Tame Topology and O-Minimal Structures, London Mathematical Society Lecture Note Series, vol. 248, Cambridge University Press, Cambridge, 1998.Google Scholar
Ziegler, M., Introduction to the lascar group, Tits Buildings and the Model Theory of Groups (Tent, K., editor), London Mathematical Society Lecture Note Series, vol. 291, Cambridge University Press, Cambridge, 2002, pp. 279–298.10.1017/CBO9780511549786.013CrossRefGoogle Scholar