Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bartoszynski, Tomek
and
Judah, Haim
1990.
Jumping with random reals.
Annals of Pure and Applied Logic,
Vol. 48,
Issue. 3,
p.
197.
Judah, Haim
and
Shelah, Saharon
1990.
Around random algebra.
Archive for Mathematical Logic,
Vol. 30,
Issue. 3,
p.
129.
Judah, Haim
1992.
Set Theory of the Continuum.
Vol. 26,
Issue. ,
p.
75.
Judah, Haim
and
Shelah, Saharon
1993.
Adding dominating reals with the random algebra.
Proceedings of the American Mathematical Society,
Vol. 119,
Issue. 1,
p.
267.
Keremedis, Kyriakos
1995.
On the covering and the additivity number of the real line.
Proceedings of the American Mathematical Society,
Vol. 123,
Issue. 5,
p.
1583.

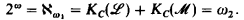 .
.