Article contents
Complete theories with countably many rigid nonisomorphic models1
Published online by Cambridge University Press: 12 March 2014
Extract
Here we prove the following:
Theorem. For every N ≤ ω there is a complete theory Tn having exactly n nonisomorphic rigid models and no uncountable rigid models. Moreover, each non-rigid model admits a nontrivial automorphism.
The Tn are theories in the first-order predicate calculus and a rigid structure is a structure with no nontrivial endomorphisms, i.e., the only endomorphism of the structure into itself is the identity. The theorem answers a question of A. Ehrenfeucht.
For the most part we use standard model theoretic notation with Th 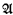 denoting the set of sentences true in
denoting the set of sentences true in 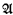 and
and  meaning
meaning  . A complete set of sentences is one of the form Th
. A complete set of sentences is one of the form Th 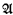 for some
for some 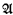 . The universe of a structure
. The universe of a structure 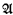 may be denoted by ∣
may be denoted by ∣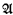 ∣. An n-ary relation on X is a set of n tuples (x0, …, xn−1) with each xi ∈ X. All the structures encounted here will be relational. If P is an n-ary relation then P ↾ Y, the restriction of P to Y, is {(x0, …, xn−1): (x0, …, xn−1) ∈ P and x0, …, xn−1Y}.
∣. An n-ary relation on X is a set of n tuples (x0, …, xn−1) with each xi ∈ X. All the structures encounted here will be relational. If P is an n-ary relation then P ↾ Y, the restriction of P to Y, is {(x0, …, xn−1): (x0, …, xn−1) ∈ P and x0, …, xn−1Y}.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1975
Footnotes
This work was supported in part by NSF grant GP-28070.
References
REFERENCES
- 1
- Cited by

