Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-25T04:46:11.698Z Has data issue: false hasContentIssue false
  • English
  • Français

Computably categorical structures and expansions by constants

Published online by Cambridge University Press:  12 March 2014

Peter Cholak ,
Sergey Goncharov ,
Bakhadyr Khoussainov  and
Richard A. Shore
Peter Cholak
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN, 46556, USA. E-mail: Peter.Cholak.1@nd.edu
Sergey Goncharov
Affiliation:
Department of Mathematics, Novosibirsk University, Novosibirsk, Russia E-mail: gonchar@imi.nsu.nsk.su
Bakhadyr Khoussainov
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853., USA Department of Computer Science, University of Auckland, Auckland, New Zealand E-mail: bmk@cs.auckland.ac.nz
Richard A. Shore
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853., USA E-mail: shore@math.cornell.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Effective model theory is the subject that analyzes the typical notions and results of model theory to determine their effective content and counterparts. The subject has been developed both in the former Soviet Union and in the west with various names (recursive model theory, constructive model theory, etc.) and divergent terminology. (We use “effective model theory” as the most general and descriptive designation. Harizanov [6] is an excellent introduction to the subject as is Millar [13].) The basic subjects of model theory include languages, structures, theories, models and various types of maps between these objects. There are many ways to introduce considerations of effectiveness into the area. The two most prominent derive from starting, on the one hand, with the notion of a theory and its models or, on the other, with just structures.

If one begins with theories, then a natural version of effectiveness is to consider decidable theories (i.e., ones with a decidable (equivalently, computable or recursive) set of theorems). When one moves to models and wants them to be effective, one might start with the requirement that the model 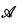(of any theory) have a decidable theory (i.e., Th (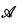), the set of sentences true in 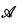, is decidable). Typically, however, one wants to be able to talk about the elements of the model as well as its theory in the given language. Thus one naturally considers the model as a structure for the language expanded by adding a constant ai, for each element ai of 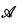. Of course, one requires that the mapping from the constants to the corresponding elements of 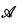be effective (computable). We are thus lead to the following basic definition:

A structure or model 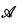is decidable if there is a computable enumeration ai of A, the domain of 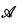, such that Th(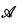, ai,) is decidable. (Of course, ai, is interpreted as ai, for each i Є ω.)

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 1 , March 1999 , pp. 13 - 37
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Crossley, J. N. (editor), Aspects of effective algebra, Upside Down A Book, Yarra Glen, 1981, Proceedings of a conference at Monash University, Australia, 1–4 08, 1979.Google Scholar
[2]Ershov, Yu. and Goncharov, S. S. (editors), Logic notebook: problems in mathematical logic, Novosibirsk University, 1986.Google Scholar
[3]Fröhlich, A. and Shepherdson, J. C., Effective procedures infield theory, Philosophical Transactions of the Royal Society of London, vol. 248 (1956), pp. 407–432.Google Scholar
[4]Goncharov, S. S., The problem of the number of non-self-equivalent constructivizations, Algebra i Logika, vol. 19 (1980), pp. 621–639.Google Scholar
[5]Grzegorczyk, A., On the definitions of computable real continuous functions, Fundamenta Mathematicae, vol. 44 (1957), pp. 61–71.CrossRefGoogle Scholar
[6]HARIZANOV, V., Pure recursive model theory, Handbook of recursive mathematics (Ershov, Y, Goncharov, S., Nerode, A., and Remmel, J., editors), to appear.Google Scholar
[7]HARIZANOV, V., The possible Turing degree of a nonzero member in a two element degree spectrum, Annals of Pure and Applies Logic, vol. 60 (1993), pp. 1–30.Google Scholar
[8]Harrington, L., Recursively presentable prime models, this Journal, vol. 39 (1974), pp. 305–309.Google Scholar
[9]Khisamiev, N., On strongly constructive models of decidable theories, Izvestiya kademiya Nauk Kazakhstan SSR, vol. 1 (1974), pp. 83–94.Google Scholar
[10]Khoussainov, B. and Shore, R., Computable isomorphisms, degree spectra of relations, and Scott families,to appear in Annals of Pure and Applied Logic.Google Scholar
[11]Lacombe, D., Extension de la notion de function recursive aux functions d’une ou plussiers variables réelles, Comptes Rendus de l’Académic des Sciences, Paris, vol. 240 (1955), pp. 151–153.Google Scholar
[12]Mal‘cev, A. I., Constructive algebras I, Uspekhi Matemematischeskoe Nauk, vol. 16 (1961), pp. 3–60.Google Scholar
[13]Millar, T., Abstract recursive model theory, Handbook of recursion theory, (Griffor, E., editor), North-Holland, to appear.Google Scholar
[14]Millar, T., Recursive categoricity and persistence, this Journal, vol. 51 (1986), pp. 430–434.Google Scholar
[15]Rabin, M. O., Computable algebra, general theory and theory of computable fields, Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
[16]Remmel, J. B. and Crossley, J. N., The work of Anil Nerode: a retrospective, Logical methods (Crossley, J. N., Remmel, J. B., Shore, R. A., and Sweedler, M. E., editors), Birkhäuser,Boston, 1993, pp. 1–91.Google Scholar