Article contents
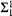 -definability at uncountable regular cardinals
-definability at uncountable regular cardinals
Published online by Cambridge University Press: 12 March 2014
Abstract
Let κ be an infinite cardinal. A subset of (κ κ)n is a 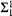 -subset if it is the projection p[T] of all cofinal branches through a subtree T of (>κ κ)n+1 of height κ. We define
-subset if it is the projection p[T] of all cofinal branches through a subtree T of (>κ κ)n+1 of height κ. We define 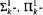 and
and 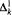 -subsets of (κ κ)n as usual.
-subsets of (κ κ)n as usual.
Given an uncountable regular cardinal κ with κ = κ <κ and an arbitrary subset A of κ κ, we show that there is a <κ-closed forcing ℙ that satisfies the κ +-chain condition and forces A to be a 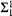 -subset of κ κ in every ℙ-generic extension of V. We give some applications of this result and the methods used in its proof.
-subset of κ κ in every ℙ-generic extension of V. We give some applications of this result and the methods used in its proof.
(i) Given any set x, we produce a partial order with the above properties that forces x to be an element of L 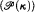 .
.
(ii) We show that there is a partial order with the above properties forcing the existence of a well-ordering of κ κ whose graph is a  -subset of κ κ × κ κ.
-subset of κ κ × κ κ.
(iii) We provide a short proof of a result due to Mekler and Väänänen by using the above forcing to add a tree T of cardinality and height κ such that T has no cofinal branches and every tree from the ground model of cardinality and height κ without a cofinal branch quasi-order embeds into T.
(iv) We will show that generic absoluteness for 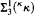 -formulae (i.e., formulae with parameters which define
-formulae (i.e., formulae with parameters which define  -subsets of κ κ) under <κ-closed forcings that satisfy the κ +-chain condition is inconsistent.
-subsets of κ κ) under <κ-closed forcings that satisfy the κ +-chain condition is inconsistent.
In another direction, we use methods from the proofs of the above results to show that 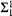 - and
- and 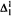 -subsets have some useful structural properties in certain ZFC-models.
-subsets have some useful structural properties in certain ZFC-models.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2012
References
REFERENCES
- 14
- Cited by

