No CrossRef data available.
Article contents
Definable incompleteness and Friedberg splittings
Published online by Cambridge University Press: 12 March 2014
Abstract
We define a property R(A0, A1) in the partial order 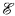 of computably enumerable sets under inclusion, and prove that R implies that A0 is noncomputable and incomplete. Moreover, the property is nonvacuous. and the A0 and A1 which we build satisfying R form a Friedberg splitting of their union A, with A1 prompt and A promptly simple. We conclude that A0 and A1 lie in distinct orbits under automorphisms of
of computably enumerable sets under inclusion, and prove that R implies that A0 is noncomputable and incomplete. Moreover, the property is nonvacuous. and the A0 and A1 which we build satisfying R form a Friedberg splitting of their union A, with A1 prompt and A promptly simple. We conclude that A0 and A1 lie in distinct orbits under automorphisms of 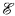 , yielding a strong answer to a question previously explored by Downey, Stob, and Soare about whether halves of Friedberg splittings must lie in the same orbit.
, yielding a strong answer to a question previously explored by Downey, Stob, and Soare about whether halves of Friedberg splittings must lie in the same orbit.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002
References
REFERENCES
[1]Cholak, P., Automorphisms of the lattice of recursively enumerable sets, Memoirs of the American Mathematical Society, vol. 113 (1995), no. 541.CrossRefGoogle Scholar
[2]Cholak, P., Downey, R., and Stob, M., Automorphisms of the lattice of recursively enumerable sets: Promptly simple sets, Transactions of the American Mathematical Society, vol. 332 (1993). pp. 555–569.CrossRefGoogle Scholar
[3]Downey, R. and Stob, M., Jumps of hemimaximal sets, Zeitschrift für Math. Logik Grundlagen, vol. 37 (1991), pp. 113–120.CrossRefGoogle Scholar
[4]Downey, R. and Stob, M., Automorphisms of the lattice of recursively enumerable sets: Orbits, Advances in Mathematics, vol. 92 (1992), pp. 237–265.CrossRefGoogle Scholar
[5]Downey, R. and Stob, M., Friedberg splittings of recursively enumerable sets, Annals of Pure and Applied Logic, vol. 59 (1993), pp. 175–199.CrossRefGoogle Scholar
[6]Friedberg, R. M., Two recursively enumerable sets of incomparable degrees of unsolvability, Proceedings of the National Academy of Sciences, USA, vol. 43 (1957), pp. 236–238.CrossRefGoogle ScholarPubMed
[7]Harrington, L. and Soare, R. I., Post's program and incomplete recursively enumerable sets, Proceedings of the National Academy of Sciences, USA, vol. 88 (1991), pp. 10242–10246.CrossRefGoogle ScholarPubMed
[8]Harrington, L. and Soare, R. I., The Δ30-automorphism method and noninvariant classes of degrees, Journal of the American Mathematical Society, vol. 9 (1996). pp. 617–666.CrossRefGoogle Scholar
[9]Harrington, L. and Soare, R. I., Definable properties of the computably enumerable sets, Annals of Pure and Applied Logic, vol. 94 (1998), pp. 97–125.CrossRefGoogle Scholar
[10]Jockusch, C. G. Jr., Review of Lerman [11], Mathematical Reviews, vol. 45 (1973). #3200.Google Scholar
[11]Lerman, M., Some theorems on r-maximal sets and major subsets of recursively enumerable sets, this Journal, vol. 36 (1971). pp. 193–215.Google Scholar
[12]Maass, W. and Stob, M., The intervals of the lattice of recursively enumerable sets determined by major subsets, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 189–212.CrossRefGoogle Scholar
[13]Muchnik, A. A., On the unsolvability of the problem of reducibilily in the theory of algorithms, Dokl. Akad. Nauk SSSR, N. S., vol. 109 (1956). pp. 194–197, in Russian.Google Scholar
[14]Myhill, J., The lattice of recursively enumerable sets, this Journal, vol. 21 (1956). pp. 215, 220.Google Scholar
[15]Rogers, H. Jr., Theory of recursive functions and effective computability, The MIT Press, Cambridge, Massachusetts, 1987.Google Scholar
[16]Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, New York, 1987.CrossRefGoogle Scholar

