Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chapuis, Olivier
and
Koiran, Pascal
1999.
Saturation and stability in the theory of computation over the reals.
Annals of Pure and Applied Logic,
Vol. 99,
Issue. 1-3,
p.
1.
Baldwin, John
and
Benedikt, Michael
2000.
Stability theory, permutations of indiscernibles, and embedded finite models.
Transactions of the American Mathematical Society,
Vol. 352,
Issue. 11,
p.
4937.
Lion, Jean-Marie
and
Speissegger, Patrick
2000.
Analytic stratification in the Pfaffian closure of an o-minimal structure.
Duke Mathematical Journal,
Vol. 103,
Issue. 2,
Tressl, Marcus
2006.
Pseudo completions and completions in stages of o-minimal structures.
Archive for Mathematical Logic,
Vol. 45,
Issue. 8,
p.
983.
ONSHUUS, ALF
and
STEINHORN, CHARLES
2009.
ON LINEARLY ORDERED STRUCTURES OF FINITE RANK.
Journal of Mathematical Logic,
Vol. 09,
Issue. 02,
p.
201.
Urquhart, Alasdair
2009.
2009 North American Annual Meeting of the Association for Symbolic Logic.
The Bulletin of Symbolic Logic,
Vol. 15,
Issue. 4,
p.
441.
Lion, Jean-Marie
and
Speissegger, Patrick
2010.
The theorem of the complement for nested sub-Pfaffian sets.
Duke Mathematical Journal,
Vol. 155,
Issue. 1,
Augustin, Doris
2012.
The Membership Problem for finitely generated quadratic modules in the univariate case.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 10,
p.
2204.
Lion, Jean-Marie
and
Speissegger, Patrick
2013.
Hausdorff limits of Rolle leaves.
Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas,
Vol. 107,
Issue. 1,
p.
79.
Ramakrishnan, Janak
2014.
Definable functions continuous on curves in o-minimal structures.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 7-8,
p.
1339.
Chernikov, Artem
and
Simon, Pierre
2015.
Externally definable sets and dependent pairs II.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 7,
p.
5217.
Yao, Ningyuan
and
Long, Dongyang
2015.
Topological dynamics for groups definable in real closed field.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 3,
p.
261.
Pillay, Anand
and
Yao, Ningyuan
2016.
On minimal flows, definably amenable groups, and o-minimality.
Advances in Mathematics,
Vol. 290,
Issue. ,
p.
483.
Cubides Kovacsics, Pablo
and
Delon, Françoise
2016.
Definable types in algebraically closed valued fields.
Mathematical Logic Quarterly,
Vol. 62,
Issue. 1-2,
p.
35.
Baizhanov, Bektur S.
2016.
One-types in ordered theories.
Vol. 1759,
Issue. ,
p.
020073.
Brouette, Quentin
2017.
Definable types in the theory of closed ordered differential fields.
Archive for Mathematical Logic,
Vol. 56,
Issue. 1-2,
p.
119.
Point, Françoise
2018.
Definability of types and VC density in differential topological fields.
Archive for Mathematical Logic,
Vol. 57,
Issue. 7-8,
p.
809.
Walsberg, Erik
2019.
The Marker–Steinhorn Theorem via Definable Linear Orders.
Notre Dame Journal of Formal Logic,
Vol. 60,
Issue. 4,
Cubides Kovacsics, Pablo
and
Ye, Jinhe
2021.
Pro-definability of spaces of definable types.
Proceedings of the American Mathematical Society, Series B,
Vol. 8,
Issue. 15,
p.
173.
Walsberg, Erik
2021.
Externally definable quotients and NIP expansions of the real ordered additive group.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 3,
p.
1551.
 -minimal theories
-minimal theories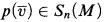 is definable if and only if for any L-formula
is definable if and only if for any L-formula 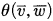 , there is an LM-formula
, there is an LM-formula 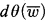 so that for all
so that for all 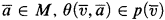 iff M ⊨ dθ(¯). The formula dθ is called the definition of θ.
iff M ⊨ dθ(¯). The formula dθ is called the definition of θ.
