We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the Turing degrees of prime models of complete decidable theories. In particular we show that every complete decidable atomic theory has a prime model whose elementary diagram is low. We combine the construction used in the proof with other constructions to show that complete decidable atomic theories have low prime models with added properties.
If we have a complete decidable atomic theory with all types of the theory computable, we show that for every degree d with 0 < d < 0', there is a prime model with elementary diagram of degree d. Indeed, this is a corollary of the fact that if T is a complete decidable theory and L is a computable set of c.e. partial types of T, then for any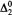 
degree d > 0, T has a d-decidable model omitting the nonprincipal types listed by L.
Email your librarian or administrator to recommend adding this journal to your organisation's collection.
