Article contents
DEGREES OF CATEGORICITY AND SPECTRAL DIMENSION
Published online by Cambridge University Press: 01 May 2018
Abstract
A Turing degree d is the degree of categoricity of a computable structure  ${\cal S}$ if d is the least degree capable of computing isomorphisms among arbitrary computable copies of
${\cal S}$ if d is the least degree capable of computing isomorphisms among arbitrary computable copies of  ${\cal S}$. A degree d is the strong degree of categoricity of
${\cal S}$. A degree d is the strong degree of categoricity of  ${\cal S}$ if d is the degree of categoricity of
${\cal S}$ if d is the degree of categoricity of  ${\cal S}$, and there are computable copies
${\cal S}$, and there are computable copies 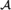 ${\cal A}$ and
${\cal A}$ and  ${\cal B}$ of
${\cal B}$ of  ${\cal S}$ such that every isomorphism from
${\cal S}$ such that every isomorphism from 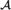 ${\cal A}$ onto
${\cal A}$ onto  ${\cal B}$ computes d. In this paper, we build a c.e. degree d and a computable rigid structure
${\cal B}$ computes d. In this paper, we build a c.e. degree d and a computable rigid structure 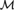 ${\cal M}$ such that d is the degree of categoricity of
${\cal M}$ such that d is the degree of categoricity of 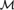 ${\cal M}$, but d is not the strong degree of categoricity of
${\cal M}$, but d is not the strong degree of categoricity of 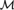 ${\cal M}$. This solves the open problem of Fokina, Kalimullin, and Miller [13].
${\cal M}$. This solves the open problem of Fokina, Kalimullin, and Miller [13].
For a computable structure  ${\cal S}$, we introduce the notion of the spectral dimension of
${\cal S}$, we introduce the notion of the spectral dimension of  ${\cal S}$, which gives a quantitative characteristic of the degree of categoricity of
${\cal S}$, which gives a quantitative characteristic of the degree of categoricity of  ${\cal S}$. We prove that for a nonzero natural number N, there is a computable rigid structure
${\cal S}$. We prove that for a nonzero natural number N, there is a computable rigid structure 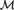 ${\cal M}$ such that
${\cal M}$ such that 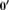 $0\prime$ is the degree of categoricity of
$0\prime$ is the degree of categoricity of 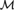 ${\cal M}$, and the spectral dimension of
${\cal M}$, and the spectral dimension of 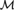 ${\cal M}$ is equal to N.
${\cal M}$ is equal to N.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 10
- Cited by

