Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Stukachev, Alexey
2006.
Theory and Applications of Models of Computation.
Vol. 3959,
Issue. ,
p.
772.
Stukachev, A. I.
2007.
Degrees of presentability of structures. I.
Algebra and Logic,
Vol. 46,
Issue. 6,
p.
419.
Reimann, Jan
2008.
Effectively closed sets of measures and randomness.
Annals of Pure and Applied Logic,
Vol. 156,
Issue. 1,
p.
170.
Kalantari, Iraj
and
Welch, Larry
2008.
On Turing degrees of points in computable topology.
Mathematical Logic Quarterly,
Vol. 54,
Issue. 5,
p.
470.
Bienvenu, Laurent
Muchnik, Andrej
Shen, Alexander
and
Vereshchagin, Nikolay
2010.
Limit Complexities Revisited.
Theory of Computing Systems,
Vol. 47,
Issue. 3,
p.
720.
Gherardi, Guido
2011.
Alan Turing and the Foundations of Computable Analysis.
The Bulletin of Symbolic Logic,
Vol. 17,
Issue. 3,
p.
394.
Bienvenu, Laurent
Gács, Peter
Hoyrup, Mathieu
Rojas, Cristobal
and
Shen, Alexander
2011.
Algorithmic tests and randomness with respect to a class of measures.
Proceedings of the Steklov Institute of Mathematics,
Vol. 274,
Issue. 1,
p.
34.
McNicholl, Timothy H.
2012.
An Effective Carathéodory Theorem.
Theory of Computing Systems,
Vol. 50,
Issue. 4,
p.
579.
Brattka, Vasco
Gherardi, Guido
and
Hölzl, Rupert
2015.
Probabilistic computability and choice.
Information and Computation,
Vol. 242,
Issue. ,
p.
249.
Simpson, Stephen G.
and
Stephan, Frank
2015.
Cone avoidance and randomness preservation.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 6,
p.
713.
Rute, Jason
2016.
Computable randomness and betting for computable probability spaces.
Mathematical Logic Quarterly,
Vol. 62,
Issue. 4-5,
p.
335.
Porter, Michelle
Day, Adam
and
Downey, Rodney
2017.
Notes on Computable Analysis.
Theory of Computing Systems,
Vol. 60,
Issue. 1,
p.
53.
Hoyrup, Mathieu
2017.
Genericity of Weakly Computable Objects.
Theory of Computing Systems,
Vol. 60,
Issue. 3,
p.
396.
Pauly, Arno
2018.
Sailing Routes in the World of Computation.
Vol. 10936,
Issue. ,
p.
328.
Miller, Joseph S.
and
Soskova, Mariya I.
2018.
Density of the cototal enumeration degrees.
Annals of Pure and Applied Logic,
Vol. 169,
Issue. 5,
p.
450.
KIHARA, TAKAYUKI
2019.
ON A METRIC GENERALIZATION OF THE tt-DEGREES AND EFFECTIVE DIMENSION THEORY.
The Journal of Symbolic Logic,
Vol. 84,
Issue. 2,
p.
726.
Andrews, Uri
Ganchev, Hristo
Kuyper, Rutger
Lempp, Steffen
Miller, Joseph
Soskova, Alexandra
and
Soskova, Mariya
2019.
On cototality and the skip operator in the enumeration degrees.
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 3,
p.
1631.
Andrews, Uri
Igusa, Gregory
Miller, Joseph S.
and
Soskova, Mariya I.
2019.
Characterizing the continuous degrees.
Israel Journal of Mathematics,
Vol. 234,
Issue. 2,
p.
743.
Kihara, Takayuki
2020.
The Brouwer invariance theorems in reverse mathematics.
Forum of Mathematics, Sigma,
Vol. 8,
Issue. ,
Greenberg, Noam
Miller, Joseph S.
and
Nies, André
2021.
Highness properties close to PA completeness.
Israel Journal of Mathematics,
Vol. 244,
Issue. 1,
p.
419.
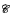 [0,1] computes a non-computable subset of ℕ there is a non-total degree between Turing degrees a <Tb iff b is a PA degree relative to a;
[0,1] computes a non-computable subset of ℕ there is a non-total degree between Turing degrees a <Tb iff b is a PA degree relative to a; 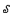 ⊆ 2ℕ is a Scott set iff it is the collection of f-computable subsets of ℕ for some f ∈
⊆ 2ℕ is a Scott set iff it is the collection of f-computable subsets of ℕ for some f ∈ 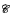 [0,1] of non-total degree; and there are computably incomparable f, g ∈
[0,1] of non-total degree; and there are computably incomparable f, g ∈ 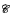 [0,1] which compute exactly the same subsets of ℕ. Proofs draw from classical analysis and constructive analysis as well as from computability theory.
[0,1] which compute exactly the same subsets of ℕ. Proofs draw from classical analysis and constructive analysis as well as from computability theory.
