Article contents
Delineating classes of computational complexity via second order theories with weak set existence principles. I
Published online by Cambridge University Press: 12 March 2014
Abstract
In this paper we characterize the well-known computational complexity classes of the polynomial time hierarchy as classes of provably recursive functions (with graphs of suitable bounded complexity) of some second order theories with weak comprehension axiom schemas but without any induction schemas (Theorem 6). We also find a natural relationship between our theories and the theories of bounded arithmetic 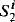 (Lemmas 4 and 5). Our proofs use a technique which enables us to “speed up” induction without increasing the bounded complexity of the induction formulas. This technique is also used to obtain an interpretability result for the theories of bounded arithmetic
(Lemmas 4 and 5). Our proofs use a technique which enables us to “speed up” induction without increasing the bounded complexity of the induction formulas. This technique is also used to obtain an interpretability result for the theories of bounded arithmetic 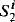 (Theorem 4).
(Theorem 4).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 1
- Cited by

