Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-18T10:43:09.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Classifying model-theoretic properties

Published online by Cambridge University Press:  12 March 2014

Chris J. Conidis
Chris J. Conidis*
Affiliation:
Department of Mathematics, University of Chicago, 5734 S. University Avenue Chicago, Illinois 60637, USA, E-mail: conidis@math.uchicago.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In 2004 Csima, Hirschfeldt, Knight, and Soare [1] showed that a set A ≤T 0′ is nonlow2 if and only if A is prime bounding, i.e., for every complete atomic decidable theory T, there is a prime model 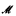computable in A. The authors presented nine seemingly unrelated predicates of a set A, and showed that they are equivalent for 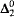sets. Some of these predicates, such as prime bounding, and others involving equivalence structures and abelian p-groups come from model theory, while others involving meeting dense sets in trees and escaping a given function come from pure computability theory.

As predicates of A, the original nine properties are equivalent for 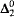sets; however, they are not equivalent in general. This article examines the (degree-theoretic) relationship between the nine properties. We show that the nine properties fall into three classes, each of which consists of several equivalent properties. We also investigate the relationship between the three classes, by determining whether or not any of the predicates in one class implies a predicate in another class.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 3 , September 2008 , pp. 885 - 905
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Csima, B. F., Hirschfeldt, D. R., Knight, J. F., and Soare, R. I., Bounding prime models, this Journal, vol. 69 (2004), pp. 1117–1142.Google Scholar
[2]Hirschfeldt, D. R., Shore, R. A., and Slaman, T. A., The atomic model theorem, to appear.Google Scholar
[3]Khisamiev, N. G., A constructibitity criterion for the direct product of cyclic p-groups, Izvestiya Akademii Nauk Kazakhskoǐ SSR. Seriya Fiziko-Matematicheskaya, (1981), pp. 51–55.Google Scholar
[4]Khisamiev, N. G., Theory of Abelian groups with constructive models, Siberian Mathematical Journal, vol. 27 (1986), pp. 572–585.CrossRefGoogle Scholar
[5]Khisamiev, N. G., Constructive Abelian groups, Handbook of recursive mathematics (Ershov, Yu. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), Studies in Logic and the Foundation of Mathematics, vol. 138-139, North Holland, Amsterdam, 1998, pp. 1177–1231.Google Scholar
[6]Khoussainov, B., Nibs, A., and Shore, R. A., Computable models of theories with few models, Notre Dame Journal of Formal Logic, vol. 38 (1997), pp. 165–178.CrossRefGoogle Scholar
[7]Lerman, M., Degrees of unsolvability, Springer-Verlag, Berlin, 1983.CrossRefGoogle Scholar
[8]Nies, A., A new spectrum of recursive models, Notre Dame Journal of Formal Logic, vol. 40 (1999), pp. 307–314.CrossRefGoogle Scholar
[9]Shinoda, J. and Slaman, T. A., Recursive in a generic real, this Journal, vol. 65 (2000), pp. 164–172.Google Scholar
[10]Soare, R. I., Recursively enumerable sets and degrees: A study of computable functions and computably generated sets, Springer-Verlag, Heidelberg, 1987.CrossRefGoogle Scholar