Article contents
Dual weak pigeonhole principle, pseudo-surjective functions, and provability of circuit lower bounds
Published online by Cambridge University Press: 12 March 2014
Abstract
This article is a continuation of our search for tautologies that are hard even for strong propositional proof systems like EF. cf. [14, 15]. The particular tautologies we study, the τ-formulas. are obtained from any 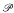 /poly map g; they express that a string is outside of the range of g, Maps g considered here are particular pseudorandom generators. The ultimate goal is to deduce the hardness of the τ-formulas for at least EF from some general, plausible computational hardness hypothesis.
/poly map g; they express that a string is outside of the range of g, Maps g considered here are particular pseudorandom generators. The ultimate goal is to deduce the hardness of the τ-formulas for at least EF from some general, plausible computational hardness hypothesis.
In this paper we introduce the notions of pseudo-surjective and iterable functions (related to free functions of [15]). These two properties imply the hardness of the τ-formulas from the function but unlike the hardness they are preserved under composition and iteration. We link the existence of maps with these two properties to the provability of circuit lower bounds, and we characterize maps g yielding hard τ-formulas in terms of a hitting set type property (all relative to a propositional proof system). We show that a proof system containing EF admits a pseudo-surjective function unless it simulates a proof system WF introduced by Jeřábek [11]. an extension of EF.
We propose a concrete map g as a candidate function possibly pseudo-surjective or free for strong proof systems. The map is defined as a Nisan-Wigderson generator based on a random function and on a random sparse matrix. We prove that it is iterable in a particular way in resolution, yielding the output/input ratio n3 −ε (that improves upon a direct construction of Alekhnovich et al. [2]).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2004
References
REFERENCES
- 28
- Cited by

