Article contents
THE EIGHTFOLD WAY
Published online by Cambridge University Press: 01 May 2018
Abstract
Three central combinatorial properties in set theory are the tree property, the approachability property and stationary reflection. We prove the mutual independence of these properties by showing that any of their eight Boolean combinations can be forced to hold at 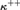 ${\kappa ^{ + + }}$, assuming that
${\kappa ^{ + + }}$, assuming that 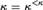 $\kappa = {\kappa ^{ < \kappa }}$ and there is a weakly compact cardinal above κ.
$\kappa = {\kappa ^{ < \kappa }}$ and there is a weakly compact cardinal above κ.
If in addition κ is supercompact then we can force κ to be 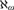 ${\aleph _\omega }$ in the extension. The proofs combine the techniques of adding and then destroying a nonreflecting stationary set or a
${\aleph _\omega }$ in the extension. The proofs combine the techniques of adding and then destroying a nonreflecting stationary set or a 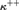 ${\kappa ^{ + + }}$-Souslin tree, variants of Mitchell’s forcing to obtain the tree property, together with the Prikry-collapse poset for turning a large cardinal into
${\kappa ^{ + + }}$-Souslin tree, variants of Mitchell’s forcing to obtain the tree property, together with the Prikry-collapse poset for turning a large cardinal into 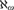 ${\aleph _\omega }$.
${\aleph _\omega }$.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 10
- Cited by

