Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cenzer, Douglas
Harizanov, Valentina
and
Remmel, Jeffrey B.
2009.
Mathematical Theory and Computational Practice.
Vol. 5635,
Issue. ,
p.
99.
Cenzer, Douglas
Harizanov, Valentina
and
Remmel, Jeffrey B.
2011.
Σ10 and Π10 equivalence structures.
Annals of Pure and Applied Logic,
Vol. 162,
Issue. 7,
p.
490.
Cenzer, Douglas
Harizanov, Valentina
and
Remmel, Jeffrey B.
2011.
Models of Computation in Context.
Vol. 6735,
Issue. ,
p.
51.
Calvert, Wesley
Miller, Russell
and
Reimann, Jennifer Chubb
2013.
Approximating functions and measuring distance on a graph.
p.
24.
Cenzer, D.
Harizanov, V.
and
Remmel, J. B.
2013.
Two-to-one structures.
Journal of Logic and Computation,
Vol. 23,
Issue. 6,
p.
1195.
Fokina, Ekaterina B.
Harizanov, Valentina
and
Melnikov, Alexander
2014.
Turing's Legacy.
p.
124.
Cenzer*, D.
Harizanov**, V.
and
Remmel***, J. B.
2014.
Computability-Theoretic Properties of Injection Structures.
Algebra and Logic,
Vol. 53,
Issue. 1,
p.
39.
Bazhenov, N. A.
2015.
The Branching Theorem and Computable Categoricity in the Ershov Hierarchy.
Algebra and Logic,
Vol. 54,
Issue. 2,
p.
91.
Calvert, Wesley
Cenzer, Douglas
Harizanov, Valentina
Brattka, Vasco
Greenberg, Noam
Kalimullin, Iskander
and
Soskova, Mariya
2022.
Generically and coarsely computable isomorphisms.
Computability,
Vol. 11,
Issue. 3-4,
p.
223.

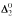 -categoricity is equivalent to our notion of graph-
-categoricity is equivalent to our notion of graph-