Hostname: page-component-5c6d5d7d68-sv6ng Total loading time: 0 Render date: 2024-08-17T05:11:49.873Z Has data issue: false hasContentIssue false
  • English
  • Français

Extending the Curry-Howard interpretation to linear, relevant and other resource logics1

Published online by Cambridge University Press:  12 March 2014

Dov M. Gabbay  and
Ruy J. G. B. de Queiroz
Dov M. Gabbay
Affiliation:
Department of Computing, Imperial College of Science, Technology and Medicine, University of London, London SW7 2BZ, United Kingdom, E-mail: dg@doc.ic.ac.uk
Ruy J. G. B. de Queiroz
Affiliation:
Department of Computing, Imperial College of Science, Technology and Medicine, University of London, London SW7 2BZ, United Kingdom, E-mail: rjq@doc.ic.ac.uk
Get access Rights & Permissions [Opens in a new window]

Extract

The so-called Curry-Howard interpretation (Curry [1934], Curry and Feys [1958], Howard [1969], Tait [1965]) is known to provide a rather neat term-functional account of intuitionistic implication. Could one refine the interpretation to obtain an almost as good account of other neighbouring implications, including the so-called ‘resource’ implications (e.g. linear, relevant, etc.)?

We answer this question positively by demonstrating that just by working with side conditions on the rule of assertability conditions for the connective representing implication (‘→’) one can characterise those ‘resource’ logics. The idea stems from the realisation that whereas the elimination rule for conditionals (of which implication is a particular case) remains virtually unchanged no matter what kind of conditional one has (i.e. linear, relevant, intuitionistic, classical, etc., all have modus ponens), the corresponding introduction rule carries an element of vagueness which can be explored in the characterisation of several sorts of conditionals. The rule of →-introduction is classified as an ‘improper’ inference rule, to use a terminology from Prawitz [1965]. Now, the so-called improper rules leave room for manoeuvre as to how a particular logic can be obtained just by imposing conditions on the discharge of assumptions that would correspond to the particular logical discipline one is adopting (linear, relevant, ticket entailment, intuitionistic, classical, etc.). The side conditions can be ‘naturally’ imposed, given that a degree of ‘vagueness’ is introduced by the presentation of those improper inference rules, such as the rule of →-introduction:

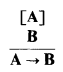
which says: starting from assumption ‘A’, and arriving at ‘B’ via an unspecified number of steps, one can discharge the assumption and conclude that ‘A’ implies ‘B’.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 4 , December 1992 , pp. 1319 - 1365
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

A preliminary version of this paper was presented at the Informal Logic Colloquium, held at the Seminar für Natürlich-sprachliche Systeme (SNS), Universität Tübingen, on March 21–22, 1990, and has appeared in one volume of the series SNS-Berichte edited by P. Schroeder-Heister. Later, a more developed version was presented at Logic Colloquium '90, the European Summer Meeting of the Association for Symbolic Logic, Helsinki, Finland, July 15–22, 1990, the abstract of which appeared in this Journal, vol. 56(1991), pp. 1139–1140.

References

REFERENCES

Ajdukiewicz, Kazimierz [1935], Die syntaktische Konnexität, Studia Philosophica, vol. 1, pp. 1–27; English translation, Syntactic connexion, Polish Logic 1920–1939 (Storrs McCail, editor), Clarendon, Press, Oxford, 1967, pp. 207–231.Google Scholar
Anderson, Alan R. and Belnap, Nuel D. Jr. [1975], Entailment. The logic of relevance and necessity, Volume I (with contributions by Dunn, J. Michael & Meyer, Robert K.), Princeton University Press, Princeton, New Jersey.Google Scholar
Barendregt, Henk P. [1981], The lambda calculus. Its syntax and semantics (revised edition 1984), Studies in Logic and The Foundations of Mathematics, vol. 103, North-Holland, Amsterdam.Google Scholar
van Benthem, Johan [1989], Categorial grammar and type theory, Journal of Philosophical Logic, vol. 18, pp. 116–168.Google Scholar
van Benthem, Johan [1990], Categorial grammar meets unification, to appear in Unification formalisms: syntax, semantics and implementation (Wedekind, J. et al., editors). It should be obtainable from the author at Institute for Language, Logic and Information, Dept. of Mathematics and Computer Science, Plantage Muidergracht 24, NL-1018 TV Amsterdam, The Netherlands (final version, 02 1990).Google Scholar
Chellas, Brian F. [1980], Modal logic. An introduction, Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Church, Alonzo [1941], The calculi of lambda-conversion (second printing 1951), Annals of Mathematics Studies (Emil Artin and Marston Morse, editors), no. 6, Princeton University Press, Princeton, New Jersey.Google Scholar
Curry, Haskell B. [1931], The universal quantifier in combinatory logic, Annals of Mathematics, vol. 32, pp. 154–180.CrossRefGoogle Scholar
Curry, Haskell B. [1934], Functionality in combinatory logic, Proceedings of the National Academy of Sciences of the United States of America, vol. 20, pp. 584–590.CrossRefGoogle ScholarPubMed
Curry, Haskell B. [1942], The combinatory foundations of mathematical logic, this Journal, vol. 7, pp. 49–64.Google Scholar
Curry, Haskell B. [1950], A theory of formal deducibility (second edition 1957, third printing 1966), Notre Dame Mathematical Lectures (O'Meara, O. T. and Stoll, Wilhelm, editors), no. 6, Notre Dame, Indiana.Google Scholar
Curry, Haskell B. [1963], Foundations of mathematical logic (reprinted with corrections 1977), Dover Publications, New York.Google Scholar
Curry, Haskell B. and Feys, Robert [1958], Combinatory logic, vol. I, Studies in Logic and The Foundations of Mathematics, North-Holland, Amsterdam.Google Scholar
Curry, Haskell B., Hindley, J. Roger and Seldin, Jonathan P. [1972], Combinatory logic, vol. II, Studies in Logic and The Foundations of Mathematics, North-Holland, Amsterdam.Google Scholar
Došen, Kosta [1988], Sequent systems and grupoid models, Studia Logica, vol. 47, pp. 353–385.CrossRefGoogle Scholar
Došen, Kosta [1989], Sequent systems and grupoid models II, Studia Logica, vol. 48, pp. 41–65.CrossRefGoogle Scholar
Fitch, Frederic B. [1952], Symbolic logic. An introduction, Ronald Press, New York.Google Scholar
Frege, Gottlob [1879], Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens, Verlag von Louis Nebert, Halle; English translation, Begriffsschrift, a formula language, modeled upon that of arithmetic, for pure thought, in van Heijenoort (editor) [ 1967], pp. 1–82.Google Scholar
Frege, Gottlob [1891], Funktion und Begriff, first published in the Proceedings of the Jena medical and scientific society, 1981; English translation, P. Geach, Function and concept, Collected papers on mathematics, logic and philosophy (B. McGuinness, editor) (M. Black, V. H. Dudman, P. Geach, H. Kaal, E.-H. W. Kludge, B. McGuinness, R. H. Stoothoff, and Basil Blackwell, translators), Oxford, pp. 137–156.Google Scholar
Frege, Gottlob [1893], Grundgesetze der Arithmetik. I, Verlag von Hermann Pohle, Jena. Reprinted in Olms Paperbacks, Band 32, Georg Olms Verlagsbuchhandlung, Hildesheim, 1966. Partial English translation in Furth (editor) [1964].Google Scholar
Furth, Montgomery (editor) [1964], The basic laws of arithmetic. Exposition of the system (partial English translation of Gottlob Frege's Grundgesetze der Arithmetik), University of California Press, Berkeley and Los Angeles.Google Scholar
Gabbay, Dov M. [1988], What is negation in a system?, Proceedings of logic colloquium '86 (Kingston-upon-Hull, UK) (Drake, F. R. and Truss, J. K., editors), Studies in Logic and The Foundations of Mathematics, North-Holland, Amsterdam, pp. 95–112.Google Scholar
Gabbay, Dov M. [1989], LDS—labelled deductive systems, preprint, Department of Computing, Imperial College, London, SW7 2BZ, UK, first draft September 1989, current draft February 1991. Published as CIS-Bericht-90-22, Centrum für Informations- and Sprachverarbeitung, Universität München, Germany. Final version to appear as a book with Oxford University Press.Google Scholar
Gabbay, Dov M. [1990], Labelled deductive systems: A position paper, Logic colloquium '90, Springer-Verlag (to appear).Google Scholar
Gabbay, Dov. M. and de Queiroz, Ruy J. G. B. [1991a], An attempt at the functional interpretation of the model necessity, first draft 03 11, 1991 (presented at MEDLAR 18-month Workshop, Torino. Italy, April 27–May 1, 1991), current draft 05 17, 1991.Google Scholar
Gabbay, Dov. M. [1991b], The functional interpretation and the sequent calculus (in preparation).Google Scholar
Girard, Jean-Yves [1971], Une extension de l'interprétation de Godei à l'analyse, et son application à l'élimination des coupures dans l'analyse et la theorie des types, Proceedings of the second Scandinavian logic symposium, (Oslo, June 18–201970) (Fenstad, J., editor), Studies in Logic and The Foundations of Mathematics, vol. 63, North-Holland, Amsterdam, pp. 63–92.CrossRefGoogle Scholar
Girard, Jean-Yves [1987], Linear logic, Theoretical Computer Science, vol. 50, pp. 1–102.CrossRefGoogle Scholar
Girard, Jean-Yves, Lafont, Yves and Taylor, Paul [1989], Proofs and types (reprinted with minor corrections 1990), Cambridge Tracts in Theoretical Computer Science (van Rijsbergen, C. J., managing editor), no. 7, Cambridge University Press, Cambridge.Google Scholar
Godel, Kurt [1958], Über eine bisher noch nicht benützte Erweiterung des finiten Standpunktes, Dialectica, vol. 12, pp. 280–287; English translation, On a hitherto unexploited extension of the finitary standpoint, Journal of Philosophical Logic, vol. 9 (1980), pp. 133–142.CrossRefGoogle Scholar
Goodman, Nicolas D. [1970], A theory of constructions equivalent to arithmetic, Intuitionism and proof theory, Proceedings of the summer conference at Buffalo, New York, 1968 (Kino, A., Myhill, J. and Vesley, R. E., editors), Studies in Logic and The Foundations of Mathematics, North-Holland, pp. 101–120.Google Scholar
Grzegorczyk, Andrej [1967], Some relational systems and the associated topological spaces, Fundamenta Mathematicae, vol. 60, pp. 223–231.CrossRefGoogle Scholar
Heijenoort, Jean van (editor) [1967], From Frege to Gödei: A source hook in mathematical logic. 1879–1931, Source Books in the History of the Sciences (Madden, Edward H., general editor), Harvard University Press, Cambridge, Massachusetts.Google Scholar
Helman, Glen H. [1977], Restricted lambda abstraction and the interpretation of some non-classical logics, Ph.D. dissertation, University of Pittsburgh.Google Scholar
Heyting, Arend [1946], On weakened quantification, this Journal, vol. 11, pp. 119–121.Google Scholar
Heyting, Arend [1956], Intuitionism. An introduction, Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam.Google Scholar
Hilbert, D. and Ackermann, W. [1938], Grundzüge der Theoretischen Logik, 2nd edition, Berlin; English translation, Principles of mathematical logic (edited with notes by R. E. Luce), Chelsea, New York, 1950.CrossRefGoogle Scholar
Hindley, J. Roger and Meredith, David [1990], Principal type-schemes and condensed detachment, this Journal, vol. 55, pp. 90–105.Google Scholar
Hindley, J. Roger and Seldin, Jonathan P. [1986], Introduction to combinators and λ-calculus, London Mathematical Society Student Texts, (Davies, E. B., managing editor), vol. 1, Cambridge University Press, Cambridge.Google Scholar
Howard, William A. [1969], The formulae-as-types notion of construction, privately circulated notes, only later published in To H. B. Curry: Essays on combinatory logic, lambda calculus and formalism (Seldin, J. P. and Hindley, J. R., editors), Academic Press, London, 1980, pp. 479–490.Google Scholar
Howard, William A. [1991], Review of Girard, Lafont and Taylor's Proofs and types, this Journal, vol. 56, pp. 760–761.Google Scholar
Jaśkowski, Stanisław [1934], On the rules of suppositions in formal logic, Studia Logica, vol. 1, pp. 5–32; reprinted in Polish Logic 1920–1939 (S. McCall, editor), Clarendon Press, Oxford, 1967, pp. 232–258.Google Scholar
Johansson, Ingebrigt [1936], Der Minimalkalkül, ein reduzierter intuitionistischer Formalismus, Compositie Mathematica, vol. 4, pp. 119–136.Google Scholar
Komori, Yuichi [1983], The variety generated by BCC-algebras is finitely based, Reports of Faculty of Science, Shizuoka University, vol. 17, pp. 13–16.Google Scholar
Komori, Yuichi [1989a], Illative combinatory logic based on BCK-logic, Mathematica Japonka, vol. 34, no. 4, pp. 585–596.Google Scholar
Komori, Yuichi [1989b], On BB'I logic, BB'IK logic and BB'IW logic (handwritten manuscript), 27 02 1989. (It should be obtainable from the author at Department of Mathematics, Faculty of Science, Shizuoka University, Ohya, Shizuoka 422, Japan.)Google Scholar
Komori, Yuichi [1990(?)], BI logic and its related logics, handwritten memo. (See Komori [1989b] above.)Google Scholar
Lambek, Joachim [1958], The mathematics of sentence structure, American Mathematical Monthly, vol. 65, pp. 154–170.CrossRefGoogle Scholar
Lambek, Joachim [1980], From λ-calculus to cartesian closed categories, To H. B. Curry: Essays on combinatory logic, lambda calculus and formalism (Seldin, J. P. and Hindley, J. R., editors), Academic Press, London, pp. 375–402.Google Scholar
Lambek, Joachim [1989], Multicategories revisited, Contemporary Mathematics, vol. 92, pp. 217–239.CrossRefGoogle Scholar
Lambek, Joachim and Scott, P. J. [1986], Introduction to higher order categorical logic, Cambridge Studies in Advanced Mathematics (Garling, D. J. H., Gorenstein, D., Dieck, T. Tom, and Walters, P., editorial board), vol. 7, Cambridge University Press, Cambridge.Google Scholar
Läuchli, H. [1965], Intuitionistic prepositional calculus and definably non-empty terms (abstract), this Journal, vol. 30, p. 263.Google Scholar
Läuchli, H. [1970], An abstract notion of realizability for which intuitionistic predicate calculus is complete, Intuitionism and proof theory, Proceedings of the summer conference at Buffalo, New York, 1968 (Kino, A., Myhill, J. and Vesley, R. E., editors), Studies in Logic and The Foundations of Mathematics, North-Holland, Amsterdam, pp. 227–234.Google Scholar
Łukasiewicz, J. and Tarski, A. [1930], Untersuchungen über den Aussagenkalkül, Comptes rendus des séances de la Société des Sciences et des Lettres de Varsovie, Classe III, vol. 23, pp. 30–50.Google Scholar
Martin-Löf, Per [1972], Infinite terms and a system of natural deduction, Compositie Mathematica, vol. 24, pp. 93–103.Google Scholar
Martin-Löf, Per [1975], An intuitionistic theory of types: predicative part, Proceedings of the logic colloquium '73 (Bristol, UK) (Rose, H. E. and Shepherdson, J. C., editors), Studies in Logic and The Foundations of Mathematics, vol. 80, North-Holland, Amsterdam, pp. 73–118.CrossRefGoogle Scholar
Martin-Löf, Per [1982], Constructive mathematics and computer programming, Proceedings of the international congress for logic, methodology and philosophy of science VI (Hannover, August 22–29, 1979) (Cohen, L. J., Łos, J., Pfeiffer, H. and Podewski, K.-P., editors), Studies in Logic and The Foundations of Mathematics, North-Holland, Amsterdam, 1982, pp. 153–175.Google Scholar
Martin-Löf, Per [1984], Intuitionistic type theory (notes by Giovanni Sambin of a series of lectures given in Padova, 06 1980), Studies of Proof Theory, Bibliopolis, Naples.Google Scholar
Martin-Löf, Per [1985], On the meanings of the logical constants and the justifications of the logical laws, Atti degli incontri di logica matematica, vol. 2 (Bernardi, C. and Pagli, P., editors), Scuola di Specializzazione in Logica Matematica, Dipartimento di Matematica, Università di Siena, pp. 203–281.Google Scholar
Ono, Hiroakira [1988], Structural rules and a logical hierarchy, preprint, Faculty of Integrated Arts and Sciences, Hiroshima University, Higashisendamachi, Hiroshima 730, Japan, 11 pp. (To appear in the Proceedings, of the summer school and conference on mathematical logic Heyting '88, held at Varna, Bulgaria.)Google Scholar
Ono, Hiroakira & Komori, Yuichi [1985], Logics without the contraction rule, this Journal, vol. 50, pp. 169–201.Google Scholar
Peano, Giuseppe [1889], Arithmetices principia, nova methodo exposita, Turin; English translation, The principles of arithmetic, presented by a new method, in Heijenoort, van (editor) [1967], pp. 83–97.Google Scholar
Prawitz, Dag [1965], Natural deduction. A proof-theoretical study, Acta Universitatis Stock-holmiensis. Stockholm Studies in Philosophy 3, Almqvist & Wiksell, Stockholm.Google Scholar
Prawitz, Dag [1971], Ideas and results in proof theory, Proceedings of the second Scandinavian logic symposium (Oslo, June 18–20,1970) (Fenstad, Jens E., editor), Studies in Logic and The Foundations of Mathematics, vol. 63, North-Holland, Amsterdam, pp. 235–307.CrossRefGoogle Scholar
de Queiroz, Ruy J. G. B. [1988], A proof-theoretic account of programming and the rôle of reduction rules, Dialectica, vol. 42, no. 4, pp. 265–282. (MR 90b:03090)CrossRefGoogle Scholar
de Queiroz, Ruy J. G. B. [1989], The mathematical language and its semantics: to show the consequences of a proposition is to give its meaning, Reports of the thirteenth international Wittgenstein symposium 1988 (Weingartner, P. and Schurz, G., editors), Schriftenreihe der Wittgenstein-Gesellschaft, vol. 18 (Leinfellner, E., Haller, R., Hübner, A., Leinfellner, W. and Weingartner, P., editors), Hölder-Pichler-Tempsky, Vienna, pp. 259–266.Google Scholar
de Queiroz, Ruy J. G. B. [1990], Normalisation and the semantics of use (abstract), this Journal, vol. 55, p. 425.Google Scholar
de Queiroz, Ruy J. G. B. [1991], Meaning as grammar plus consequences, Dialectica, vol. 45, fase. 1, pp. 83–86.CrossRefGoogle Scholar
de Queiroz, Ruy J. G. B. and Gabbay, Dov M. [1991a], The functional interpretation of the existential quantifier, Logic colloquium '91, Uppsala, Sweden, 08 7–14, 1991. (Abstract to appear in this Journal.)Google Scholar
de Queiroz, Ruy J. G. B. [1991b], Labelled natural deduction, preliminary draft 06 20, 1991.Google Scholar
de Queiroz, Ruy J. G. B. [1991c], The functional interpretation and prepositional equality (in preparation).Google Scholar
de Queiroz, Ruy J. G. B. and Maibaum, Thomas S. E. [1990], Proof theory and computer programming, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 36, pp. 389–414.CrossRefGoogle Scholar
de Queiroz, Ruy J. G. B. [1991], Abstract data types and type theory: theories as types, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 37, pp. 149–166.CrossRefGoogle Scholar
de Queiroz, Ruy J. G. B. and Symth, Michael B. [1989], Induction rules for non-inductive types in type theory (presented at the Fifth British colloquium for theoretical computer science, Royal Holloway and Bedford New College, Egham, Surrey, UK, 04 11–13, 1989). (Abstract to appear in the Bulletin of European Association for Theoretical Computer Science (EATCS).)Google Scholar
Quine, Willard V. O. [1950], Methods of logic (4th edition 1982), Harvard University Press, Cambridge, Massachussetts.Google Scholar
Reynolds, John C. [1974], Towards a theory of type structure, Proceedings of the collogue sur la programmation (Paris), Lecture Notes in Computer Science, vol. 19, Springer-Verlag, Berlin and New York, pp. 408–425.Google Scholar
Rose, Alan [1956], Formalisation du calcul propositionnel implicatif à m valeurs de Łukasiewicz, Comptes rendus ébdomadaires des séances de l'Académie des Sciences, vol. 243, pp. 1263–1264.Google Scholar
Schönfinkel, Moses [1924], Über die Bausteine der mathematischen Logik, Mathematische Annalen, vol. 92, pp. 305–316; English translation, On the building blocks of mathematical logic, in van Heijenoort (editor) [1967], pp. 355–366.CrossRefGoogle Scholar
Scott, Dana S. [1970], Constructive validity, Proceedings of the symposium on automated deduction (Versailles, December 1968) (Laudet, M., Lacombe, D., Nolin, L. and Schützenberger, M., editors), Lecture Notes in Mathematics, vol. 125, Springer-Verlag, Berlin and New York, pp. 237–275.Google Scholar
Seldin, Jonathan P. [1989], Normalization and excluded middle. I, Studia Logica, vol. 48, pp. 193–217.CrossRefGoogle Scholar
Tait, William W. [1965], Infinitely long terms of transfinite type, Formal systems and recursive functions (Proceedings of the logic colloquium '63, held in Oxford, UK) (Crossley, J. N. and Dummett, M. A. E., editors), Studies in Logic and The Foundations of Mathematics, North-Holland, Amsterdam, pp. 176–185.CrossRefGoogle Scholar
Tait, William W. [1967], Intensional interpretations of functionals of finite type I, this Journal, vol. 32, pp. 198–212.Google Scholar
Tait, William W. [1983], Against intuitionism: constructive mathematics is part of classical mathematics, Journal of Philosophical Logic, vol. 12, pp. 173–195.CrossRefGoogle Scholar
Tuziak, Roman [1988], An axiomatization of the finite-valued Łukasiewicz calculus, Studia Logica, vol. 47, pp. 49–55.CrossRefGoogle Scholar
Wansing, Heinrich [1990], Formulas-as-types for a hierarchy of sublogics of intuitionistic propositional logic, technical report 9/90, Berichte der Gruppe “Logik, Wissenstheorie und Information” (Pearce, David, editor).Google Scholar