Article contents
FACTORIALS OF INFINITE CARDINALS IN ZF PART I: ZF RESULTS
Published online by Cambridge University Press: 04 November 2019
Abstract
For a set x, let 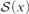 ${\cal S}\left( x \right)$ be the set of all permutations of x. We prove in ZF (without the axiom of choice) several results concerning this notion, among which are the following:
${\cal S}\left( x \right)$ be the set of all permutations of x. We prove in ZF (without the axiom of choice) several results concerning this notion, among which are the following:
(1) For all sets x such that 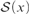 ${\cal S}\left( x \right)$ is Dedekind infinite,
${\cal S}\left( x \right)$ is Dedekind infinite, 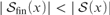 $\left| {{{\cal S}_{{\rm{fin}}}}\left( x \right)} \right| < \left| {{\cal S}\left( x \right)} \right|$ and there are no finite-to-one functions from
$\left| {{{\cal S}_{{\rm{fin}}}}\left( x \right)} \right| < \left| {{\cal S}\left( x \right)} \right|$ and there are no finite-to-one functions from 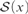 ${\cal S}\left( x \right)$ into
${\cal S}\left( x \right)$ into 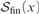 ${{\cal S}_{{\rm{fin}}}}\left( x \right)$, where
${{\cal S}_{{\rm{fin}}}}\left( x \right)$, where 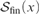 ${{\cal S}_{{\rm{fin}}}}\left( x \right)$ denotes the set of all permutations of x which move only finitely many elements.
${{\cal S}_{{\rm{fin}}}}\left( x \right)$ denotes the set of all permutations of x which move only finitely many elements.
(2) For all sets x such that 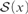 ${\cal S}\left( x \right)$ is Dedekind infinite,
${\cal S}\left( x \right)$ is Dedekind infinite, 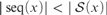 $\left| {{\rm{seq}}\left( x \right)} \right| < \left| {{\cal S}\left( x \right)} \right|$ and there are no finite-to-one functions from
$\left| {{\rm{seq}}\left( x \right)} \right| < \left| {{\cal S}\left( x \right)} \right|$ and there are no finite-to-one functions from 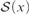 ${\cal S}\left( x \right)$ into seq (x), where seq (x) denotes the set of all finite sequences of elements of x.
${\cal S}\left( x \right)$ into seq (x), where seq (x) denotes the set of all finite sequences of elements of x.
(3) For all infinite sets x such that there exists a permutation of x without fixed points, there are no finite-to-one functions from 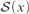 ${\cal S}\left( x \right)$ into x.
${\cal S}\left( x \right)$ into x.
(4) For all sets x, 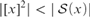 $|{[x]^2}| < \left| {{\cal S}\left( x \right)} \right|$.
$|{[x]^2}| < \left| {{\cal S}\left( x \right)} \right|$.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 9
- Cited by

