Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
2007.
Residuated Lattices: An Algebraic Glimpse at Substructural Logics.
Vol. 151,
Issue. ,
p.
463.
2007.
Residuated Lattices: An Algebraic Glimpse at Substructural Logics.
Vol. 151,
Issue. ,
p.
479.
van Alten, C. J.
2009.
Completion and finite embeddability property for residuated ordered algebras..
Algebra universalis,
Vol. 62,
Issue. 4,
p.
419.
Raftery, J. G.
2011.
Contextual Deduction Theorems.
Studia Logica,
Vol. 99,
Issue. 1-3,
p.
279.
Raftery, J. G.
2011.
A perspective on the algebra of logic.
Quaestiones Mathematicae,
Vol. 34,
Issue. 3,
p.
275.
Cardona, R.
and
Galatos, N.
2015.
The finite embeddability property for noncommutative knotted extensions of RL.
International Journal of Algebra and Computation,
Vol. 25,
Issue. 03,
p.
349.
Horčík, Rostislav
2015.
Word problem for knotted residuated lattices.
Journal of Pure and Applied Algebra,
Vol. 219,
Issue. 5,
p.
1548.
Cardona, Riquelmi
and
Galatos, Nikolaos
2017.
The FEP for some varieties of fully distributive knotted residuated lattices.
Algebra universalis,
Vol. 78,
Issue. 3,
p.
363.
Gil-Férez, José
Spada, Luca
Tsinakis, Constantine
and
Zhou, Hongjun
2020.
Join-completions of partially ordered algebras.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 10,
p.
102842.
Gil-Férez, José
Jipsen, Peter
and
Metcalfe, George
2020.
Structure theorems for idempotent residuated lattices.
Algebra universalis,
Vol. 81,
Issue. 2,
Raftery, James G.
2022.
Hiroakira Ono on Substructural Logics.
Vol. 23,
Issue. ,
p.
27.
Horčík, Rostislav
2022.
Hiroakira Ono on Substructural Logics.
Vol. 23,
Issue. ,
p.
273.

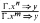 . It is proved that the class of algebraic models for such a logic has the
. It is proved that the class of algebraic models for such a logic has the 