Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jipsen, P.
and
Tsinakis, C.
2002.
Ordered Algebraic Structures.
Vol. 7,
Issue. ,
p.
19.
Okada, Mitsuhiro
2002.
A uniform semantic proof for cut-elimination and completeness of various first and higher order logics.
Theoretical Computer Science,
Vol. 281,
Issue. 1-2,
p.
471.
Kanovich, Max I
Okada, Mitsuhiro
and
Scedrov, Andre
2003.
Phase semantics for light linear logic.
Theoretical Computer Science,
Vol. 294,
Issue. 3,
p.
525.
Ono, Hiroakira
and
Ueda, Masaki
2003.
Philosophical Dimensions of Logic and Science.
p.
3.
Ono, Hiroakira
2003.
Trends in Logic.
Vol. 21,
Issue. ,
p.
193.
Van Alten, Clint J.
and
Raftery, James G.
2004.
Rule Separation and Embedding Theorems for Logics Without Weakening.
Studia Logica,
Vol. 76,
Issue. 2,
p.
241.
Belardinelli, Francesco
Jipsen, Peter
and
Ono, Hiroakira
2004.
Algebraic Aspects of Cut Elimination.
Studia Logica,
Vol. 77,
Issue. 2,
p.
209.
Dal Lago, Ugo
and
Martini, Simone
2004.
Phase semantics and decidability of elementary affine logic.
Theoretical Computer Science,
Vol. 318,
Issue. 3,
p.
409.
Farulewski, Maciej
2005.
On Finite Models of the Lambek Calculus.
Studia Logica,
Vol. 80,
Issue. 1,
p.
63.
Dyckhoff, Roy
and
Negri, Sara
2006.
Decision methods for linearly ordered Heyting algebras.
Archive for Mathematical Logic,
Vol. 45,
Issue. 4,
p.
411.
van Alten, C. J.
2006.
On Varieties of Biresiduation Algebras.
Studia Logica,
Vol. 83,
Issue. 1-3,
p.
425.
Galatos, Nikolaos
and
Ono, Hiroakira
2006.
Algebraization, Parametrized Local Deduction Theorem and Interpolation for Substructural Logics over FL.
Studia Logica,
Vol. 83,
Issue. 1-3,
p.
279.
2007.
Residuated Lattices: An Algebraic Glimpse at Substructural Logics.
Vol. 151,
Issue. ,
p.
479.
Okada, Mitsuhiro
and
Takemura, Ryo
2007.
Rewriting, Computation and Proof.
Vol. 4600,
Issue. ,
p.
167.
2007.
Residuated Lattices: An Algebraic Glimpse at Substructural Logics.
Vol. 151,
Issue. ,
p.
463.
Olson, J.S.
Raftery, J.G.
and
Van Alten, C.J.
2008.
Structural Completeness in Substructural Logics.
Logic Journal of IGPL,
Vol. 16,
Issue. 5,
p.
453.
Iorgulescu, Afrodita
2008.
On BCK algebras: Part II: New algebras. The ordinal sum (product) of two bounded BCK algebras.
Soft Computing,
Vol. 12,
Issue. 9,
p.
835.
Buszkowski, Wojciech
and
Farulewski, Maciej
2009.
Languages: From Formal to Natural.
Vol. 5533,
Issue. ,
p.
45.
Kozak, Michał
2009.
Distributive Full Lambek Calculus Has the Finite Model Property.
Studia Logica,
Vol. 91,
Issue. 2,
p.
201.
Galatos, Nikolaos
and
Ono, Hiroakira
2010.
Cut elimination and strong separation for substructural logics: An algebraic approach.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 9,
p.
1097.
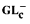 of Ono [11], that will settle the open problems stated in Ono [12].
of Ono [11], that will settle the open problems stated in Ono [12].
