Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-25T19:16:27.645Z Has data issue: false hasContentIssue false
  • English
  • Français

General models, descriptions, and choice in type theory

Published online by Cambridge University Press:  12 March 2014

Peter B. Andrews
Peter B. Andrews*
Affiliation:
Carnegie-Mellon University, Pittsburgh, Pennsylvania 15213
Get access Rights & Permissions [Opens in a new window]

Extract

In [4] Alonzo Church introduced an elegant and expressive formulation of type theory with λ-conversion. In [8] Henkin introduced the concept of a general model for this system, such that a sentence A is a theorem if and only if it is true in all general models. The crucial clause in Henkin's definition of a general model ℳ is that for each assignment φ of values in ℳ to variables and for each wff A, there must be an appropriate value 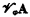of A in ℳ. Hintikka points out in [10, p. 3] that this constitutes a rather strong requirement concerning the structure of a general model. Henkin draws attention to the problem of constructing nonstandard models for the theory of types in [9, p. 324].

We shall use a simple idea of combinatory logic to find a characterization of general models which does not directly refer to wffs, and which is easier to work with in certain contexts. This characterization can be applied, with appropriate minor and obvious modifications, to a variety of formulations of type theory with λ-conversion. We shall be concerned with a language ℒ with extensionality in which there is no description or selection operator, and in which (for convenience) the sole primitive logical constants are the equality symbols Qoαα for each type α.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 2 , June 1972 , pp. 385 - 394
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Andrews, Peter B., A reduction of the axioms for the theory of propositional types, Fundamenta Mathematicae, vol. 52 (1963), pp. 345–350.CrossRefGoogle Scholar
[2]Andrews, Peter B., A transfinite type theory with type variables, North-Holland, Amsterdam, 1965, 143 pp.Google Scholar
[3]Andrews, Peter B., Resolution in type theory, this Journal, vol. 36 (1971), pp. 414–432.Google Scholar
[4]Church, Alonzo, A formulation of the simple theory of types, this Journal, vol. 5 (1940), pp. 56–68.Google Scholar
[5]Church, Alonzo, Non-normal truth-tables for the propositional calculus, Boletin de la Sociedad Matematica Mexicana, vol. X (1953), pp. 41–52.Google Scholar
[6]Curry, Haskell B. and Feys, Robert, Combinatory logic, vol. 1, North-Holland, Amsterdam, 1958, 1968, 433 pp.Google Scholar
[7]Fraenkel, Abraham A., Der Begriff ‘definit’ und die Unabhängigkeit des Auswahlaxioms, Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, vol. 21 (1922), pp. 253–257; translated in Jean van Heijenoort, From Frege to Gödel, Harvard University Press, Cambridge, 1967, pp. 284–289.Google Scholar
[8]Henkin, Leon, Completeness in the theory of types, this Journal, vol. 15 (1950), pp. 81–91; reprinted in [10, pp. 51–63].Google Scholar
[9]Henkin, Leon, A theory of propositional types, Fundamenta Mathematicae, vol. 52 (1963), pp. 323–344; errata, ibid., vol. 53 (1963), p. 119.CrossRefGoogle Scholar
[10]Hintikka, Jaakko, editor, The philosophy of mathematics, Oxford University Press, Oxford, 1969, 186 pp.Google Scholar
[11]Lévy, Azriel, The Fraenkel-Mostowski method for independence proofs in set theory, The theory of models, Proceedings of the 1963 International Symposium at Berkeley, edited by Addison, J. W., Henkin, Leon, and Tarski, Alfred, North-Holland, Amsterdam, 1965, pp. 221–228.Google Scholar
[12]Mostowski, Andrzej, Über die Unabhängigkeit des Wohlordnungssatzes vom Ordnungsprinzip, Fundamenta Mathematicae, vol. 32 (1939), pp. 201–252.CrossRefGoogle Scholar
[13]Sanchis, Luis E., Types in combinatory logic, Notre Dame Journal of Formal Logic, vol. 5 (1964), pp. 161–180.CrossRefGoogle Scholar