Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-31T21:07:25.927Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry of *-Finite Types

Published online by Cambridge University Press:  12 March 2014

Ludomir Newelski
Ludomir Newelski*
Affiliation:
Mathematical Insitute, University of Wrocław, Pl. Grunwaldzki 2/4, 50-384, Wrocław, Poland Mathematical Institute of The Polish Academy of Sciences, E-mail: newelski@math.uni.wroc.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

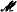Assume T is a superstable theory with < 2ℵ0 countable models. We prove that any *- algebraic type of -rank > 0 is m-nonorthogonal to a *-algebraic type of 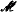-rank 1. We study the geometry induced by m-dependence on a *-algebraic type 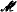p* of -rank 1. We prove that after some localization this geometry becomes projective over a division ring . Associated with p* is a meager type p. 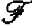We prove that p is determined by p* up to nonorthogonality and that underlies also the geometry induced by forking dependence on any stationarization of 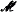p. Also we study some *-algebraic *-groups of -rank 1 and prove that any *-algebraic *-group of 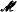-rank 1 is abelian-by-finite.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 4 , December 1999 , pp. 1375 - 1395
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[Bu1] Buechler, S., Locally modular theories of finite rank, Annals of Pure and Applied Logic, vol. 30 (1986), pp. 83–95.CrossRefGoogle Scholar
[Bu2] Buechler, S., Classification of small weakly minimal sets I, Classification theory, Proceedings, Chicago 1985 (Baldwin, J.T., editor), Springer, Berlin, 1988, pp. 32–71.Google Scholar
[Hru] Hrushovski, E., Locally modular regular types, Classification theory, Proceedings, Chicago 1985 (Baldwin, J.T., editor), Springer, Berlin, 1988, pp. 132–164.Google Scholar
[Lo] Loveys, J., Abelian groups with modular generics, this Journal, vol. 56 (1991), pp. 250–259.Google Scholar
[Ne1] Newelski, L., Flat Morley sequences, this Journal, accepted.Google Scholar
[Ne2] Newelski, L., m-normal theories, Fundamenta Mathematicae, submitted.Google Scholar
[Ne3] Newelski, L., Vaught's conjecture for some meager groups, Israel Journal of Mathematics, accepted.Google Scholar
[Ne4] Newelski, L., Weakly minimal formulas: A global approach, Annals of Pure and Applied Logic, vol. 46 (1990), pp. 65–94.CrossRefGoogle Scholar
[Ne5] Newelski, L., On type-definable subgroups of a stable group, Notre Dame Journal of Formal Logic, vol. 32 (1991), pp. 173–187.CrossRefGoogle Scholar
[Ne6] Newelski, L., A model and its subset, this Journal, vol. 57 (1992), pp. 644–658.Google Scholar
[Ne7] Newelski, L., Meager forking, Annals of Pure and Applied Logic, vol. 70 (1994), pp. 141–175.CrossRefGoogle Scholar
[Ne8] Newelski, L., -rank and meager types, Fundamenta Mathematicae, vol. 146 (1995), pp. 121–139.CrossRefGoogle Scholar
[Ne9] Newelski, L., -rank and meager groups, Fundamenta Mathematicae, vol. 150 (1996),pp. 149–171.CrossRefGoogle Scholar
[Ne1O] Newelski, L., -gap conjecture and m-normal theories, Israel Journal of Mathematics, vol. 106 (1998), pp. 285–311.CrossRefGoogle Scholar
[Ox] Oxtoby, J.C., Measure and category, Springer, Berlin, 1980.CrossRefGoogle Scholar
[Pi] Pillay, A., Geometric stability theory, Oxford, 1996.CrossRefGoogle Scholar