Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-30T07:00:59.239Z Has data issue: false hasContentIssue false
  • English
  • Français

Grzegorcyk's hierarchy and IepΣ1

Published online by Cambridge University Press:  12 March 2014

Gaisi Takeuti
Gaisi Takeuti*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, Illinois 61801, E-mail: takeuti@symcom.math.uiuc.edu
Get access Rights & Permissions [Opens in a new window]

Extract

A proof-theoretic characterization of the primitive recursive functions is the Σ1-definable functions in IΣ1 as is shown in Mints [4], Parsons [5], and [8].

Then what is a proof-theoretic characterization of Grzegorzyk's hierarchy? First we discuss a related previous work. In Clote and Takeuti [2], we introduced a theory TAC that corresponds to the computational complexity class AC. TAC has a very weak form of induction. We assign a rank to a proof in TAC in the following way. The rank of a proof P in TAC is the nesting number of inductions used in P. Then TACi is defined to be the subtheory of TAC whose proof has a rank ≤ i. We proved that TACi corresponds to the class ACi.

In this paper we introduce a theory IepΣ1 which is equivalent to IΣ1. Then we define the rank of a proof in IepΣ1 as the nesting number of inductions in the proof and prove that the proofs with rank ≤ i correspond to Grzegorcyk's hierarchy 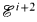for i > 0.

We also prove that the system that has proofs with rank 0 is actually equivalent to I Δ0. These facts are interesting since it is proved in [10] that the theory isomorphic to TAC∘ by RSUV isomorphism is a conservative extension of I Δo. Therefore there is some analogy between the class AC and the primitive recursive functions.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 4 , December 1994 , pp. 1274 - 1284
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Buss, S. R., Bounded arithmetic, Bibliopolis, 1986 (to appear).Google Scholar
[2]Clote, P. and Takeuti, G., First order bounded arithmetic and small boolean circuit complexity classes (to appear).Google Scholar
[3]Hájek, P. and Pudlák, P., Melamathematics of first-order arithmetic, Springer-Verlag, New York, 1993.CrossRefGoogle Scholar
[4]Mints, G. E., Quantifier-free and one-quantifier systems, Journal of Soviet Mathematics, vol. 1 (1973), pp. 71–84.CrossRefGoogle Scholar
[5]Parsons, C., On a number-theoretic choice schema and its relations to induction, Intuitionism and Proof Theory, Proceedings of the Summer Conference at Buffalo N.Y. 1968, North-Holland, Amsterdam, 1970, pp. 459–473.CrossRefGoogle Scholar
[6]Parikh, R., Existence and feasibility in arithmetic, Journal of Symbolic Logic, vol. 36 (1971), pp. 494–508.CrossRefGoogle Scholar
[7]Rose, H. E., Subrecursion: functions and hierachies, Oxford University Press, London, 1984.Google Scholar
[8]Takeuti, G., Proof Theory, vol. 2nd ed, North-Holland, Amsterdam, 1975.Google Scholar
[9]Takeuti, G., RSUV isomorphisms, Proof theory and computational complexity (Colte, P. and Krájiĉek, J., editors), Oxford University Press, London, 1993, pp. 364–386.Google Scholar
[10]Takeuti, G., RSUV isomorphisms for TACi, TNCi and TLS (to appear).Google Scholar