Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-07-06T13:26:19.908Z Has data issue: false hasContentIssue false
  • English
  • Français

HARRINGTON’S PRINCIPLE IN HIGHER ORDER ARITHMETIC

Published online by Cambridge University Press:  22 April 2015

YONG CHENG  and
RALF SCHINDLER
YONG CHENG
Affiliation:
INSTITUT FÜR MATHEMATISCHE LOGIK UND GRUNDLAGENFORSCHUNG UNIVERSITÄT MÜNSTER EINSTEINSTR. 6248149 MÜNSTER, GERMANYE-mail:world-cyr@hotmail.comE-mail:rds@math.uni-muenster.de
RALF SCHINDLER
Affiliation:
INSTITUT FÜR MATHEMATISCHE LOGIK UND GRUNDLAGENFORSCHUNG UNIVERSITÄT MÜNSTER EINSTEINSTR. 6248149 MÜNSTER, GERMANYE-mail:world-cyr@hotmail.comE-mail:rds@math.uni-muenster.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Z2, Z3, and Z4 denote 2nd, 3rd, and 4th order arithmetic, respectively. We let Harrington’s Principle, HP, denote the statement that there is a real x such that every x-admissible ordinal is a cardinal in L. The known proofs of Harrington’s theorem “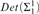$Det\left( {{\rm{\Sigma }}_1^1} \right)$ implies 0♯ exists” are done in two steps: first show that 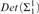$Det\left( {{\rm{\Sigma }}_1^1} \right)$ implies HP, and then show that HP implies 0♯ exists. The first step is provable in Z2. In this paper we show that Z2 + HP is equiconsistent with ZFC and that Z3 + HP is equiconsistent with ZFC + there exists a remarkable cardinal. As a corollary, Z3 + HP does not imply 0♯ exists, whereas Z4 + HP does. We also study strengthenings of Harrington’s Principle over 2nd and 3rd order arithmetic.

Keywords

03E3503E5503E30Harrington’s Principle HP0♯remarkable cardinalalmost disjoint forcingclass forcingreshapingHP (φ)subcomplete forcingRevised Countable Support (RCS) iterationsiterated club shootingZ2Z3Z4
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 2 , June 2015 , pp. 477 - 489
Copyright
Copyright © The Association for Symbolic Logic 2015 

References

REFERENCES

Barwise, J., Admissible Sets and Structures, Perspectives in Mathematical Logic, vol. 7, Springer Verlag, Berlin, 1976.Google Scholar
Beller, A., Jensen, R. B., and Welch, P., Coding the Universe, Cambridge University Press, Cambridge, 1982.Google Scholar
Cummings, James, Iterated Forcing and Elementary Embeddings,Handbook of set theory (Foreman, M. and Kanamori, A., editors), Springer Verlag, Berlin, 2010.Google Scholar
Devlin, Keith J., Constructibility, Springer, Berlin, 1984.Google Scholar
Harrington, L. A., Analytic determinacy and 0♯, this Journal, 43(1978), pp. 685–693.Google Scholar
Jech, Thomas J., Multiple forcing, Cambridge University Press, Cambridge, 1986.Google Scholar
Jech, Thomas J., Set Theory, Third millennium edition, revised and expanded, Springer, Berlin, 2003.Google Scholar
Jensen, Ronald, Iteration Theorems for Subcomplete and Related Forcings, handwritten notes, available athttp://www.mathematik.hu-berlin.de/∼raesch/org/jensen.html.Google Scholar
Jensen, Ronald, Lecture note on subcomplete forcing and L-forcing, handwritten notes, available athttp://www.mathematik.hu-berlin.de/∼raesch/org/jensen.html.Google Scholar
Kanamori, Akihiro, The Higher Infinite: Large Cardinals in Set Theory from Their Beginnings, second ed., Springer Monographs in Mathematics, Springer, Berlin, 2003.Google Scholar
Kunen, Kenneth, Set Theory: An Introduction to Independence Proofs, North Holland, Amsterdam, 1980.Google Scholar
Mansfield, R. and Weitkamp, G., Recursive Aspects of Descriptive Set Theory, Oxford University Press, Oxford, 1985.Google Scholar
Sami, Ramez L., Analytic determinacy and 0♯: A forcing-free proof of Harrington’s theorem. Fundamenta Mathematicae, vol. 160 (1999), pp. 153–159.Google Scholar
Schindler, Ralf, Coding into K by reasonable forcing. Transactions of the American Mathematical Society, vol. 353 (2000), pp. 479–489.CrossRefGoogle Scholar
Schindler, Ralf, Proper forcing and remarkable cardinals II, this Journal, vol. 66 (2001), pp. 1481–1492.Google Scholar
Schindler, Ralf, Set theory: Exploring independence and truth, Springer-Verlag, Berlin, 2014.CrossRefGoogle Scholar
Shelah, S., Proper and Improper Forcing, Perspectives in Mathematical Logic, Springer Verlag, Berlin, 1998.Google Scholar
Shelah, S. and Stanley, L., Coding and reshaping when there are no sharps, Set Theory of the Continuum (Judah, H. et al. ., editors), Springer-Verlag, New York, 1992, pp. 407–416.Google Scholar