No CrossRef data available.
Article contents
Hechler's Theorem for tall analytic P-ideals
Published online by Cambridge University Press: 12 March 2014
Abstract
We prove the following version of Hechler's classical theorem: For each partially ordered set (Q, ≤) with the property that every countable subset of Q has a strict upper bound in Q, there is a ccc forcing notion such that in the generic extension for each tall analytic P-ideal 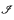 (coded in the ground model) a cofinal subset of
(coded in the ground model) a cofinal subset of 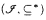 is order isomorphic to (Q, ≤).
is order isomorphic to (Q, ≤).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2011
References
REFERENCES
[1]Bartoszynski, Tomek and Kada, Masaru, Hechler's theorem for the meager ideal, Topology and its Applications, vol. 146–147 (2005), pp. 429–435.CrossRefGoogle Scholar
[2]Burke, Maxim R., A proof of Heckler's theorem on embedding ℵ1-directed sets cofinally into (ωω, <*), Archive for Mathematical Logic, vol. 36 (1997), pp. 399–403.CrossRefGoogle Scholar
[3]Burke, Maxim R. and Kada, Masaru, Hechler's theorem for the null ideal, Archive for Mathematical Logic, vol. 43 (2004), pp. 703–722.CrossRefGoogle Scholar
[4]Fremlin, David H., Measure theory. Set-theoretic measure theory, Torres Fremlin, Colchester, England, 2004, available at http://www.essex.ac.uk/maths/staff/fremlin/mt.html.Google Scholar
[5]Hechler, S. H., On the existence of certain cofinal subsets of ωω, Axiomatic set theory (Jech, Thomas, editor), American Mathematical Society, 1974, pp. 155–173.CrossRefGoogle Scholar
[6]Solecki, Slamowir, Analytic P-ideals and their applications, Annals of Pure and Applied Logic, vol. 99 (1999), pp. 51–72.CrossRefGoogle Scholar
[7]Soukup, Lajos, Pcf theory and cardinal invariants of the reals, unpublished notes, 2001.Google Scholar

