Hostname: page-component-76dd75c94c-qmf6w Total loading time: 0 Render date: 2024-04-30T08:54:05.377Z Has data issue: false hasContentIssue false
  • English
  • Français

A hierarchy of tree-automatic structures

Published online by Cambridge University Press:  12 March 2014

Olivier Finkel  and
Stevo Todorčević
Olivier Finkel
Affiliation:
Equipe De Logique Mathématique, Institut De Mathématiques De Jussieu, CNRSand Université Paris 7, France, E-mail: finkel@logique.jussieu.fr
Stevo Todorčević
Affiliation:
Equipe De Logique Mathématique, Institut De Mathématiques De Jussieu, CNRSand Université Paris 7, France Department of Mathematics, University of Toronto,Toronto, M5S 2E4, CanadaE-mail: todorcevic@math.jussieu.fr, E-mail: stevo@math.toronto.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider ωn-automatic structures which are relational structures whose domain and relations are accepted by automata reading ordinal words of length ωn for some integer n ≥ 1. We show that all these structures are ω-tree-automatic structures presentable by Muller or Rabin tree automata. We prove that the isomorphism relation for ω2-automatic (resp. ωn-automatic for n > 2) boolean algebras (respectively, partial orders, rings, commutative rings, non commutative rings, non commutative groups) is not determined by the axiomatic system ZFC. We infer from the proof of the above result that the isomorphism problem for ωn-automatic boolean algebras, n ≥ 2, (respectively, rings, commutative rings, non commutative rings, non commutative groups) is neither a 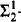-set nor a 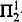-set. We obtain that there exist infinitely many ωn-automatic, hence also ω-tree-automatic, atomless boolean algebras 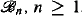, which are pairwise isomorphic under the continuum hypothesis CH and pairwise non isomorphic under an alternate axiom AT, strengthening a result of [14].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 1 , March 2012 , pp. 350 - 368
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bedon, N., Finite automata and ordinals, Theoretical Computer Science, vol. 156 (1996), no. 1–2, pp. 119–144.CrossRefGoogle Scholar
[2]Bedon, N., Logic over words on denumerable ordinals, Journal of Computer and System Science, vol. 63 (2001), no. 3, pp. 394–431.CrossRefGoogle Scholar
[3]Bedon, N. and Carton, O., An Eilenberg theorem for words on countable ordinals, Latin '98: Theoretical informatics, third Latin American symposium (Lucchesi, Claudio L. and Moura, Arnaldo V., editors), Lecture Notes in Computer Science, vol. 1380, Springer, 1998, pp. 53–64.CrossRefGoogle Scholar
[4]Belegradek, O. V., The model theory of unitriangular groups, Annals of Pure and Applied Logic, vol. 68 (1994), pp. 225–261.CrossRefGoogle Scholar
[5]Blumensath, A., Automatic structures, Diploma Thesis, RWTH, Aachen, 1999.Google Scholar
[6]Blumensath, A. and Grädel, E., Automatic structures, Proceedings of 15th IEEE symposium on Logic in Computer Science LICS 2000, 2000, pp. 51–62.Google Scholar
[7]Blumensath, A., Finite presentations of infinite structures: Automata and interpretations. Theory of Computing Systems, vol. 37 (2004), no. 6, pp. 641–674.CrossRefGoogle Scholar
[8]Bã≫Chi, J. R. and Siefkes, D., The monadic second order theory of all countable ordinals, Lecture Notes in Mathematics, vol. 328, 1973.Google Scholar
[9]Duparc, J., Finkel, O., and Ressayre, J.-P., Computer science and the fine structure of Borel sets, Theoretical Computer Science, vol. 257 (2001), no. 1–2, pp. 85–105.CrossRefGoogle Scholar
[10]Farah, I., Analytic quotients: theory of liftings for quotients over analytic ideals on the integers, Memoirs of the American Mathematical Society, vol. 148 (2000).CrossRefGoogle Scholar
[11]Farah, I., Luzin gaps, Transactions of the American Mathematical Society, vol. 356 (2004), no. 6, pp. 2197–2239, (electronic).CrossRefGoogle Scholar
[12]Farah, I., All automorphism of the Calkin algebras are inner, Annals of Mathematics, vol. 173 (2011), no. 2, pp. 619–661.CrossRefGoogle Scholar
[13]Finkel, O., Locally finite languages, Theoretical Computer Science, vol. 255 (2001), no. 1–2, pp. 223–261.CrossRefGoogle Scholar
[14]Finkel, O. and TodorčEvić, S., The isomorphism relation between tree-automatic structures, Central European Journal of Mathematics, vol. 8 (2010), no. 2, pp. 299–313.CrossRefGoogle Scholar
[15]Grädel, E., Thomas, W., and Wilke, W. (Editors), Automata, logics, and infinite games: A guide to current research, Lecture Notes in Computer Science, vol. 2500, Springer, 2002.CrossRefGoogle Scholar
[16]Hemmer, J. C., Automates sur mots de longueur supérieure á ω, Mémoire de Licence, Université de Liège, 1992.Google Scholar
[17]Hjorth, G., Khoussainov, B., Montalban, A., and Nies, A., From automatic structures to Borel structures, Proceedings of the twenty-third annual IEEE symposium on Logic in Computer Science, LICS 2008, IEEE Computer Society, Pittsburgh, PA, 2008, pp. 431–441.Google Scholar
[18]Hodgson, B. R., Décidabilité par automate fini, Anuales Scientifiques de Mathématiques du Quebec, vol. 7 (1983), no. 1, pp. 39–57.Google Scholar
[19]Hopcroft, J. E., Motwani, R., and Ullman, J. D., Introduction to automata theory, languages, and computation, Addison-Wesley Series in Computer Science, Addison-Wesley Publishing Co., Reading, Mass., 2001.Google Scholar
[20]Jech, T., Set theory, third ed., Springer, 2002.Google Scholar
[21]Just, W., A modification of Shelah's oracle-c.c. with applications, Transactions of the American Mathematical Society, vol. 329 (1992), no. 1, pp. 325–356.Google Scholar
[22]Just, W., A weak version of AT from OCA, Set theory of the continuum, Mathematical Sciences Research Institute Publications, vol. 26, Springer, 1992, pp. 281–291.CrossRefGoogle Scholar
[23]Kanovei, V. and Reeken, M., New Radon-Nikodym ideals, Mathematika, vol. 47 (2000), no. 1–2, pp. 219–227.CrossRefGoogle Scholar
[24]Kechris, A. S., Classical descriptive set theory, Springer-Verlag, New York, 1995.CrossRefGoogle Scholar
[25]Khoussainov, B. and Nerode, A., Open questions in the theory of automatic structures, Bulletin of the European Association of Theoretical Computer Science, vol. 94 (2008), pp. 181–204.Google Scholar
[26]Khoussainov, B., Nies, A., Rubin, S., and Stephan, F., Automatic structures: Richness and limitations, Logical Methods in Computer Science, vol. 3 (2007), no. 2, pp. 1–18.Google Scholar
[27]Khoussainov, B. and Rubin, S., Automatic structures: Overview and future directions, Journal of Automata, Languages and Combinatorics, vol. 8 (2003), no. 2, pp. 287–301.Google Scholar
[28]Kuske, D., Is Ramsey's Theorem omega-automatic?, 27th International Symposium on Theoretical Aspects of Computer Science, STACS 2010, Leibniz International Proceedings in Computer Science, vol. 5, Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2010, pp. 537–548.Google Scholar
[29]Kuske, D., Liu, J., and Lohrey, M., The isomorphism problem for omega-automatic trees, Proceedings of Computer Science Logic, CSL 2010, Lecture Notes in Computer Science, vol. 6247, Springer, 2010, pp. 396–410.Google Scholar
[30]Kuske, D., The isomorphism problem on classes of automatic structures, Proceedings of the 25th annual IEEE symposium on Logic in Computer Science, LICS 2010, IEEE Computer Society, 2010, pp. 160–169.CrossRefGoogle Scholar
[31]Kuske, D. and Lohrey, M., First-order and counting theories of omega-automatic structures, this Journal, vol. 73 (2008), no. 1, pp. 129–150.Google Scholar
[32]Moschovakis, Y. N., Descriptive set theory, North-Holland Publishing Co., Amsterdam, 1980.Google Scholar
[33]Nies, A., Describing groups, The Bulletin of Symbolic Logic, vol. 13 (2007), no. 3, pp. 305–339.CrossRefGoogle Scholar
[34]Perrin, D. and Pin, J.-E., Infinite words, automata, semigroups, logic and games, Pure and Applied Mathematics, vol. 141, Elsevier, 2004.Google Scholar
[35]Poizat, B., A course in model theory, Universitext, Springer-Verlag, New York, 2000.CrossRefGoogle Scholar
[36]Rabin, M. O., Decidability of second-order theories and automata on infinite trees, Transactions of the American Mathematical Society, vol. 141 (1969), pp. 1–35.Google Scholar
[37]Rotman, B., A mapping theorem for countable well-ordered sets, Journal of the London Mathematical Society. Second Series, vol. 2 (1970), pp. 509–512.CrossRefGoogle Scholar
[38]Rubin, S., Automatic structures, Ph.D. thesis, University of Auckland, 2004.Google Scholar
[39]Rubin, S., Automata presenting structures: A survey of the finite string case, The Bulletin of Symbolic Logic, vol. 14 (2008), no. 2, pp. 169–209.CrossRefGoogle Scholar
[40]Staiger, L., ω-languages, Handbook of formal languages, vol. 3, Springer, Berlin, 1997, pp. 339–387.CrossRefGoogle Scholar
[41]Talagrand, M., Compacts de fonctions mesurables et filtres non mesurables, Stadia Mathematica, vol. 67 (1980), no. 1, pp. 13–43.CrossRefGoogle Scholar
[42]Thomas, W., Automata on infinite objects, Handbook of theoretical computer science (van Leeuwen, J., editor), Formal models and semantics, vol. B, Elsevier, 1990, pp. 135–191.Google Scholar
[43]Todorčević, S., Partition problems in topology, Contemporary Mathematics, vol. 84, American Mathematical Society, Providence, R.I., 1989.CrossRefGoogle Scholar
[44]Todorčević, S., Gaps in analytic quotients, Fundamenta Mathematicae, vol. 156 (1998), no. 1, pp. 85–97.CrossRefGoogle Scholar
[45]Wojciechowski, J., Classes of transfinite sequences accepted by finite automata, Fundamenta Informaticae, vol. 7 (1984), no. 2, pp. 191–223.CrossRefGoogle Scholar
[46]Wojciechowski, J., Finite automata on transfinite sequences and regular expressions, Fundamenta Informaticae, vol. 8 (1985), no. 3–4, pp. 379–396.CrossRefGoogle Scholar