Hostname: page-component-cb9f654ff-5kfdg Total loading time: 0 Render date: 2025-08-20T11:53:53.320Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGH DIMENSIONAL COUNTABLE COMPACTNESS AND ULTRAFILTERS

Part of: Fairly general properties Set theory Generalities

Published online by Cambridge University Press:  07 April 2025

CÉSAR CORRAL Open the ORCID record for CÉSAR CORRAL [Opens in a new window] ,
POURYA MEMARPANAHI  and
PAUL JAN SZEPTYCKI Open the ORCID record for PAUL JAN SZEPTYCKI [Opens in a new window]
CÉSAR CORRAL*
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS YORK UNIVERSITY 4700 KEELE ST TORONTO, ON M3J 1P3 CANADA E-mail: pourya7@yorku.ca
POURYA MEMARPANAHI
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS YORK UNIVERSITY 4700 KEELE ST TORONTO, ON M3J 1P3 CANADA E-mail: pourya7@yorku.ca
PAUL JAN SZEPTYCKI
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS YORK UNIVERSITY TORONTO, ONTARIO M3J 1P3 CANADA E-mail: szeptyck@yorku.ca
*
E-mail: cicorral@yorku.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We define several notions of a limit point on sequences with domain a barrier in 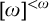$[\omega ]^{<\omega }$ focusing on the two dimensional case 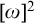$[\omega ]^2$. By exploring some natural candidates, we show that countable compactness has a number of generalizations in terms of limits of high dimensional sequences and define a particular notion of 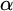$\alpha $-countable compactness for $\alpha \leq \omega _1$. We then focus on dimension 2 and compare 2-countable compactness with notions previously studied in the literature. We present a number of counterexamples showing that these classes are different. In particular assuming the existence of a Ramsey ultrafilter, a subspace of 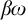$\beta \omega $ which is doubly countably compact whose square is not countably compact, answering a question of T. Banakh, S. Dimitrova, and O. Gutik [3]. The analysis of this construction leads to some possibly new types of ultrafilters related to discrete, P-points and Ramsey ultrafilters.

Keywords

countably compactRamsey ultrafilterP-pointdiscrete ultrafilterdoubly countably compactp-compactdouble sequence

MSC classification

Primary: 54D80: Special constructions of spaces (spaces of ultrafilters, etc.) 54A20: Convergence in general topology (sequences, filters, limits, convergence spaces, etc.) 54D35: Extensions of spaces (compactifications, supercompactifications, completions, etc.) 03E35: Consistency and independence results

Information

Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 21
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Balcerzak, M. and Dems, K., Some types of convergence and related Baire systems . Real Analysis Exchange, vol. 30 (2004), no. 1, pp. 267–276.Google Scholar
Banakh, T. and Blass, A., The number of near-coherence classes of ultrafilters is either finite or ${2}^{\mathfrak{c}}$ , Set Theory, (J. Bagaria and S. Todorcevic, editors), Trends in Mathematics, Birkhäuser, Basel, 2006, pp. 257–273.Google Scholar
Banakh, T. O., Dimitrova, S., and Gutik, O. V., The Rees-Suschkewitsch theorem for simple topological semigroups . Matematychni Studii, vol. 31 (2009), no. 2, pp. 211–218.Google Scholar
Banakh, T., On $\kappa$ -bounded and $M$ -compact reflections of topological spaces . Topology and its Applications, vol. 289 (2021), Paper No. 107547.Google Scholar
Baumgartner, J. E., Ultrafilters on $\omega$ . Journal of Symbolic Logic, vol. 60 (1995), no. 2, pp. 624–639.Google Scholar
Baumgartner, J. E. and Laver, R., Iterated perfect-set forcing . Annals of Mathematical Logic, vol. 17 (1979), no. 3, pp. 271–288.Google Scholar
Bernstein, A. R., A new kind of compactness for topological spaces . Fundamenta Mathematicae, vol. 66 (1969), pp. 185–193.Google Scholar
Bojańczyk, M., Kopczyński, E., and Toruńczyk, S., Ramsey’s theorem for colors from a metric space . Semigroup Forum, vol. 85 (2012), no. 1, pp. 182–184.Google Scholar
Booth, D., Ultrafilters on a countable set . Annals of Mathematical Logic, vol. 2 (1970), no. 1, pp. 1–24.Google Scholar
Comfort, W. W., Ultrafilters: Some old and some new results . Bulletin of the American Mathematical Society, vol. 83 (1977), no. 4, pp. 417–455.Google Scholar
Corral, C., Guzmán, O., López-Callejas, C., Memarpanahi, P., Szeptycki, P., and Todorčević, S., Infinite dimensional sequential compactness: Sequential compactness based on barriers . Canadian Journal of Mathematics, Published online (2024), pp. 1–28. doi:https://doi.org/10.4153/S0008414X24000646.Google Scholar
Dobrinen, N., Continuous and other finitely generated canonical cofinal maps on ultrafilters . Fundamenta Mathematicae, vol. 249 (2020), no. 2, pp. 111–147.Google Scholar
Frolík, Z., Sums of ultrafilters . Bulletin of the American Mathematical Society, vol. 73 (1967), pp. 87–91.Google Scholar
García-Ferreira, S. and Ortiz-Castillo, Y. F., Pseudocompactness and ultrafilters , Pseudocompact Topological Spaces: A Survey of Classic and New Results with Open Problems (M. Hrušák, A. Tamariz-Mascarúa, and M. Tkachenko, editors), Springer, Cham, 2018, pp. 77–105.Google Scholar
Hrušák, M. and Moore, J. T., Introduction: Twenty problems in set-theoretic topology , Open Problems in Topology II (E. Pearl, editor), Elsevier, Amsterdam, 2007, pp. 111–113.Google Scholar
Knaust, H., Angelic spaces with the Ramsey property , Interaction Between Functional Analysis, Harmonic Analysis, and Probability (Columbia, MO, 1994), (N. Kalton, E. Saab, and S. Montgomery-Smith, editors), volume 175 of Lecture Notes in Pure and Applied Mathematics, Dekker, New York, 1996, pp. 267–273.Google Scholar
Knaust, H., Array convergence of functions of the first Baire class . Proceedings of the American Mathematical Society, vol. 112 (1991), no. 2, pp. 529–532.Google Scholar
Kubiś, W. and Szeptycki, P., On a topological Ramsey theorem . Canadian Mathematical Bulletin, vol. 66 (2023), no. 1, pp. 156–165.Google Scholar
Michael, E. A., A quintuple quotient quest . General Topology and its Applications, vol. 2 (1972), pp. 91–138.Google Scholar
Novák, J., On the Cartesian product of two compact spaces . Fundamenta Mathematicae, vol. 40 (1953), pp. 106–112.Google Scholar
Nyikos, P., Soukup, L., and Veličković, B., Hereditary normality of $\gamma \boldsymbol{N}$ -spaces . Topology and Its Applications, vol. 65 (1995), no. 1, pp. 9–19.Google Scholar
Nyikos, P. J. and Vaughan, J. E., The Scarborough-Stone problem for Hausdorff spaces , Proceedings of the Symposium on General Topology and Applications (Oxford, 1989) (P. J. Collins, editor), Elsevier, Amsterdam, vol. 44, 1992, pp. 309–316.Google Scholar
Scarborough, C. T. and Stone, A. H., Products of nearly compact spaces . Transactions of the American Mathematical Society, vol. 124 (1966), pp. 131–147.Google Scholar
Terasaka, H., On Cartesian product of compact spaces . Osaka Journal of Mathematics, vol. 4 (1952), pp. 11–15.Google Scholar
Todorcevic, S., Introduction to Ramsey Spaces, volume 174 of Annals of Mathematics Studies, Princeton University Press, Princeton, 2010.Google Scholar
Vaughan, J. E., Products of perfectly normal, sequentially compact spaces . Journal of the London Mathematical Society, vols. 2–14 (1976), no. 3, pp. 517–520.Google Scholar