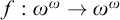1 Introduction
In [Reference Switzer8] the second author introduced 18 cardinal characteristics on the set of functions
![]() $f:\omega ^\omega \to \omega ^\omega $
generalizing standard cardinal characteristics on
$f:\omega ^\omega \to \omega ^\omega $
generalizing standard cardinal characteristics on
![]() $\omega $
by replacing relations on
$\omega $
by replacing relations on
![]() $\omega $
such as
$\omega $
such as
![]() $\leq $
by their “mod finite” counterparts, e.g.,
$\leq $
by their “mod finite” counterparts, e.g.,
![]() $\leq ^*$
and the “mod finite” quotienting by “mod
$\leq ^*$
and the “mod finite” quotienting by “mod
![]() $\mathcal I$
” where
$\mathcal I$
” where
![]() $\mathcal I$
is some well studied
$\mathcal I$
is some well studied
![]() $\sigma $
-ideal on the reals such as the ideal of meager or measure zero sets. In that article it was shown that these cardinals can be organized into two diagrams of
$\sigma $
-ideal on the reals such as the ideal of meager or measure zero sets. In that article it was shown that these cardinals can be organized into two diagrams of
![]() $\mathsf {ZFC}$
-provable relations similar to the Cichoń diagram (see below Figures 1 and 2). Several relations between these “higher dimensional” cardinals and their brethren on
$\mathsf {ZFC}$
-provable relations similar to the Cichoń diagram (see below Figures 1 and 2). Several relations between these “higher dimensional” cardinals and their brethren on
![]() $\omega $
were established as well as a number of consistency results, albeit all in the context where
$\omega $
were established as well as a number of consistency results, albeit all in the context where
![]() $\mathsf {CH}$
holds.
$\mathsf {CH}$
holds.
In this paper we look at when
![]() $\mathsf {CH}$
fails, a situation that turns out to be infinitely more flexible and interesting. Working in this context we prove, for the bounding numbers of the higher dimensional relations, that the provable inequalities from the higher Cichoń diagrams are in fact the only ones, with possibly one exception which we discuss. The proof consists of considering how standard iterated forcing models of the reals (Cohen, Random, Sacks, etc.) change the higher dimensional cardinals. We also present a result, due to the first author, that shows that, in contrast to what appeared in [Reference Switzer8], the
$\mathsf {CH}$
fails, a situation that turns out to be infinitely more flexible and interesting. Working in this context we prove, for the bounding numbers of the higher dimensional relations, that the provable inequalities from the higher Cichoń diagrams are in fact the only ones, with possibly one exception which we discuss. The proof consists of considering how standard iterated forcing models of the reals (Cohen, Random, Sacks, etc.) change the higher dimensional cardinals. We also present a result, due to the first author, that shows that, in contrast to what appeared in [Reference Switzer8], the
![]() $\mathsf {CH}$
context was not so interesting after all. We then study the dominating numbers when
$\mathsf {CH}$
context was not so interesting after all. We then study the dominating numbers when
![]() $\mathsf {CH}$
fails and establish many consistent inequalities while also exhibiting that several surprising
$\mathsf {CH}$
fails and establish many consistent inequalities while also exhibiting that several surprising
![]() $\mathsf {ZFC}$
relations hold between them that fail in the dual case. The result shows that these higher dimensional cardinals fail in a strong sense to satisfy the type of duality results that often characterize the classical cardinal characteristics on
$\mathsf {ZFC}$
relations hold between them that fail in the dual case. The result shows that these higher dimensional cardinals fail in a strong sense to satisfy the type of duality results that often characterize the classical cardinal characteristics on
![]() $\omega $
and even their higher analogues on arbitrary, regular
$\omega $
and even their higher analogues on arbitrary, regular
![]() $\kappa $
. To state these results more precisely we recall some definitions.
$\kappa $
. To state these results more precisely we recall some definitions.
Given a set X and a binary relation R on X we say that a set
![]() $A \subseteq X$
is R-bounded if there is a single
$A \subseteq X$
is R-bounded if there is a single
![]() $x \in X$
so that
$x \in X$
so that
![]() $y\mathbin{R}x$
for every
$y\mathbin{R}x$
for every
![]() $y \in A$
. We say that A is R-unbounded if it is not R-bounded. We say that
$y \in A$
. We say that A is R-unbounded if it is not R-bounded. We say that
![]() $A \subseteq X$
is R-dominating if for every
$A \subseteq X$
is R-dominating if for every
![]() $x \in X$
there is a
$x \in X$
there is a
![]() $y \in A$
so that
$y \in A$
so that
![]() $x\mathbin{R}y$
. For any such R and X we denote by
$x\mathbin{R}y$
. For any such R and X we denote by
![]() $\mathfrak b(R)$
the bounding number of R, i.e., the least size of an R-unbounded set and by
$\mathfrak b(R)$
the bounding number of R, i.e., the least size of an R-unbounded set and by
![]() $\mathfrak {d}(R)$
the dominating number of R, i.e., the least size of an R-dominating set.
$\mathfrak {d}(R)$
the dominating number of R, i.e., the least size of an R-dominating set.
We work primarily in Baire space. Recall that a slalom is a function
![]() $s:\omega \to [\omega ]^{<\omega }$
so that for all n we have
$s:\omega \to [\omega ]^{<\omega }$
so that for all n we have
![]() $|s(n)| \leq n$
. Let
$|s(n)| \leq n$
. Let
![]() $\mathcal S$
be the space of slaloms, which we treat as homeomorphic to
$\mathcal S$
be the space of slaloms, which we treat as homeomorphic to
![]() $\omega ^\omega $
by any reasonable homeomorphism. We recall the following three relations.
$\omega ^\omega $
by any reasonable homeomorphism. We recall the following three relations.
Definition 1.1. Let
![]() $x, y \in \omega ^\omega $
and s be a slalom.
$x, y \in \omega ^\omega $
and s be a slalom.
-
(1) We say that g eventually dominates f, in symbols
 $f \leq ^* g$
if for all but finitely many
$f \leq ^* g$
if for all but finitely many
 $k < \omega $
we have
$k < \omega $
we have
 $f(k) \leq g(k)$
. The bounding and dominating numbers for this relation are the classical cardinals
$f(k) \leq g(k)$
. The bounding and dominating numbers for this relation are the classical cardinals
 $\mathfrak b$
and
$\mathfrak b$
and
 $\mathfrak {d}$
, see [Reference Blass, Foreman and Kanamori2, Section 2].
$\mathfrak {d}$
, see [Reference Blass, Foreman and Kanamori2, Section 2]. -
(2) We say that g is eventually different from f, in symbols
 $f \neq ^* g$
if for all but finitely many
$f \neq ^* g$
if for all but finitely many
 $k < \omega $
we have
$k < \omega $
we have
 $f(k) \neq g(k)$
. A theorem of Miller states that
$f(k) \neq g(k)$
. A theorem of Miller states that
 $\mathfrak b(\neq ^*) = {\textrm {non}}(\mathcal M)$
and
$\mathfrak b(\neq ^*) = {\textrm {non}}(\mathcal M)$
and
 $\mathfrak {d}(\neq ^*) = {\textrm {cov}}(\mathcal M)$
where
$\mathfrak {d}(\neq ^*) = {\textrm {cov}}(\mathcal M)$
where
 $\mathcal M$
is the ideal of meager sets, see [Reference Blass, Foreman and Kanamori2, Theorem 5.9].
$\mathcal M$
is the ideal of meager sets, see [Reference Blass, Foreman and Kanamori2, Theorem 5.9]. -
(3) We say that f is eventually captured by s, in symbols
 $f \in ^* s$
if for all but finitely many
$f \in ^* s$
if for all but finitely many
 $k < \omega $
we have
$k < \omega $
we have
 $f(k) \in s(k)$
. By a theorem of Bartoszyński we have
$f(k) \in s(k)$
. By a theorem of Bartoszyński we have
 $\mathfrak b(\in ^*) = {\textrm {add}}(\mathcal N)$
and
$\mathfrak b(\in ^*) = {\textrm {add}}(\mathcal N)$
and
 $\mathfrak {d}(\in ^*) = {\textrm {cov}}(\mathcal N)$
where
$\mathfrak {d}(\in ^*) = {\textrm {cov}}(\mathcal N)$
where
 $\mathcal N$
is the ideal of Lebesgue measure zero sets, see [Reference Blass, Foreman and Kanamori2, Theorem 5.14].
$\mathcal N$
is the ideal of Lebesgue measure zero sets, see [Reference Blass, Foreman and Kanamori2, Theorem 5.14].
Throughout let
![]() $\mathcal I$
range over the ideal of Lebesgue measure zero sets, denoted
$\mathcal I$
range over the ideal of Lebesgue measure zero sets, denoted
![]() $\mathcal N$
, the ideal of meager sets, denoted
$\mathcal N$
, the ideal of meager sets, denoted
![]() $\mathcal M$
, and the ideal of
$\mathcal M$
, and the ideal of
![]() $\sigma $
-compact subsets of
$\sigma $
-compact subsets of
![]() $\omega ^\omega $
, denoted
$\omega ^\omega $
, denoted
![]() $\mathcal K$
. Note that by a well known result of Rothberger, the latter ideal can also be characterized as the ideal generated by
$\mathcal K$
. Note that by a well known result of Rothberger, the latter ideal can also be characterized as the ideal generated by
![]() $\leq ^*$
-bounded sets, see [Reference Blass, Foreman and Kanamori2, Theorem 2.8]. Let R range over
$\leq ^*$
-bounded sets, see [Reference Blass, Foreman and Kanamori2, Theorem 2.8]. Let R range over
![]() $\leq ^*$
,
$\leq ^*$
,
![]() $\neq ^*$
and
$\neq ^*$
and
![]() $\in ^*$
. Denote by
$\in ^*$
. Denote by
![]() $(\omega ^\omega )^{\omega ^\omega }$
the space of functions
$(\omega ^\omega )^{\omega ^\omega }$
the space of functions
![]() $f:\omega ^\omega \to \omega ^\omega $
. The following definition is the main object of study in the paper.
$f:\omega ^\omega \to \omega ^\omega $
. The following definition is the main object of study in the paper.
Definition 1.2. Let
![]() $\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
and
$\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
and
![]() $R \in \{\leq ^*, \neq ^*, \in ^*\}$
. Let
$R \in \{\leq ^*, \neq ^*, \in ^*\}$
. Let
![]() $f, g \in (\omega ^\omega )^{\omega ^\omega }$
, or in the case of
$f, g \in (\omega ^\omega )^{\omega ^\omega }$
, or in the case of
![]() $R = {\in}^*$
, let
$R = {\in}^*$
, let
![]() $g: \omega ^\omega \to \mathcal S$
. We define the relation
$g: \omega ^\omega \to \mathcal S$
. We define the relation
![]() $R_{\mathcal I}$
by
$R_{\mathcal I}$
by
![]() $f \mathbin{R_{\mathcal I}} g$
if and only if
$f \mathbin{R_{\mathcal I}} g$
if and only if
![]() $\{x \in \omega ^\omega \; | \; \neg (f(x) \mathbin{R} g(x))\} \in \mathcal I$
. In other words, g is an R-bound for f on an
$\{x \in \omega ^\omega \; | \; \neg (f(x) \mathbin{R} g(x))\} \in \mathcal I$
. In other words, g is an R-bound for f on an
![]() $\mathcal I$
-measure one set.
$\mathcal I$
-measure one set.
By varying
![]() $\mathcal I$
and R this definition gives nine new relations and 18 new cardinal characteristics, a bounding and dominating number for each. For readability, let us give the details below for the case of the null ideal. Similar statements hold for
$\mathcal I$
and R this definition gives nine new relations and 18 new cardinal characteristics, a bounding and dominating number for each. For readability, let us give the details below for the case of the null ideal. Similar statements hold for
![]() $\mathcal M$
and
$\mathcal M$
and
![]() $\mathcal K$
. First let’s see explicitly what each relation
$\mathcal K$
. First let’s see explicitly what each relation
![]() $R_{\mathcal I}$
is. On the two lists below let
$R_{\mathcal I}$
is. On the two lists below let
![]() $f, g:\omega ^\omega \to \omega ^\omega $
and
$f, g:\omega ^\omega \to \omega ^\omega $
and
![]() $h:\omega ^\omega \to \mathcal S$
.
$h:\omega ^\omega \to \mathcal S$
.
-
(1)
 $f \neq ^*_{\mathcal N} g$
if and only if for all but a measure zero set of
$f \neq ^*_{\mathcal N} g$
if and only if for all but a measure zero set of
 $x \in \omega ^\omega $
we have that
$x \in \omega ^\omega $
we have that
 $f (x) \neq ^* g(x)$
.
$f (x) \neq ^* g(x)$
. -
(2)
 $f \leq ^*_{\mathcal N} g$
if and only if for all but a measure zero set of
$f \leq ^*_{\mathcal N} g$
if and only if for all but a measure zero set of
 $x \in \omega ^\omega $
we have that
$x \in \omega ^\omega $
we have that
 $f(x) \leq ^* g(x)$
.
$f(x) \leq ^* g(x)$
. -
(3)
 $f \in ^*_{\mathcal N} h$
if and only if for all but a measure zero set of
$f \in ^*_{\mathcal N} h$
if and only if for all but a measure zero set of
 $x \in \omega ^\omega $
we have that
$x \in \omega ^\omega $
we have that
 $f(x) \in ^* h(x)$
.
$f(x) \in ^* h(x)$
.
For the cardinals now we get the following. Note that
![]() $\neg x \neq ^* y$
means
$\neg x \neq ^* y$
means
![]() $\exists ^\infty n \, x(n) = y(n)$
and the same for the other relations.
$\exists ^\infty n \, x(n) = y(n)$
and the same for the other relations.
-
(1)
 $\mathfrak b(\neq ^*_{\mathcal N})$
is the least size of a
$\mathfrak b(\neq ^*_{\mathcal N})$
is the least size of a
 $\neq ^*_{\mathcal N}$
-unbounded set
$\neq ^*_{\mathcal N}$
-unbounded set
 $A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for each
$A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for each
 $f:\omega ^\omega \to \omega ^\omega $
there is a
$f:\omega ^\omega \to \omega ^\omega $
there is a
 $g \in A$
so that the set of
$g \in A$
so that the set of
 $\{x \; | \; \exists ^\infty n \, g(x)(n) = f(x)(n)\}$
is not measure zero.
$\{x \; | \; \exists ^\infty n \, g(x)(n) = f(x)(n)\}$
is not measure zero. -
(2)
 $\mathfrak {d}(\neq ^*_{\mathcal N})$
is the least size of a
$\mathfrak {d}(\neq ^*_{\mathcal N})$
is the least size of a
 $\neq ^*_{\mathcal N}$
-dominating set
$\neq ^*_{\mathcal N}$
-dominating set
 $A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for every
$A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for every
 $f:\omega ^\omega \to \omega ^\omega $
there is a
$f:\omega ^\omega \to \omega ^\omega $
there is a
 $g \in A$
so that
$g \in A$
so that
 $\mu (\{x \; | \; f(x)\neq ^* g(x)\} )= 1$
.
$\mu (\{x \; | \; f(x)\neq ^* g(x)\} )= 1$
. -
(3)
 $\mathfrak b(\leq ^*_{\mathcal N})$
is the least size of a
$\mathfrak b(\leq ^*_{\mathcal N})$
is the least size of a
 $\leq ^*_{\mathcal N}$
-unbounded set
$\leq ^*_{\mathcal N}$
-unbounded set
 $A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for each
$A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for each
 $f:\omega ^\omega \to \omega ^\omega $
there is a
$f:\omega ^\omega \to \omega ^\omega $
there is a
 $g \in A$
so that the set of
$g \in A$
so that the set of
 $\{x \; | \; \exists ^\infty n \, f(x)(n) < g(x)(n)\}$
is not measure zero.
$\{x \; | \; \exists ^\infty n \, f(x)(n) < g(x)(n)\}$
is not measure zero. -
(4)
 $\mathfrak {d}(\leq ^*_{\mathcal N})$
is the least size of a
$\mathfrak {d}(\leq ^*_{\mathcal N})$
is the least size of a
 $\leq ^*_{\mathcal N}$
-dominating set
$\leq ^*_{\mathcal N}$
-dominating set
 $A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for every
$A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for every
 $f:\omega ^\omega \to \omega ^\omega $
there is a
$f:\omega ^\omega \to \omega ^\omega $
there is a
 $g \in A$
so that
$g \in A$
so that
 $\mu (\{x \; | \; f(x)\leq ^* g(x)\}) = 1$
.
$\mu (\{x \; | \; f(x)\leq ^* g(x)\}) = 1$
. -
(5)
 $\mathfrak b(\in ^*_{\mathcal N})$
is the least size of a
$\mathfrak b(\in ^*_{\mathcal N})$
is the least size of a
 $\in ^*_{\mathcal N}$
-unbounded set
$\in ^*_{\mathcal N}$
-unbounded set
 $A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for each
$A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for each
 $f:\omega ^\omega \to \mathcal S$
there is a
$f:\omega ^\omega \to \mathcal S$
there is a
 $g \in A$
so that the set of
$g \in A$
so that the set of
 $\{x \; | \; \exists ^\infty n \, g(x)(n) \notin f(x)(n)\}$
.
$\{x \; | \; \exists ^\infty n \, g(x)(n) \notin f(x)(n)\}$
. -
(6)
 $\mathfrak {d}(\in ^*_{\mathcal N})$
is the least size of a
$\mathfrak {d}(\in ^*_{\mathcal N})$
is the least size of a
 $\leq ^*_{\mathcal N}$
-dominating set
$\leq ^*_{\mathcal N}$
-dominating set
 $A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for every
$A \subseteq (\omega ^\omega )^{\omega ^\omega }$
, i.e., A is such that for every
 $f:\omega ^\omega \to \omega ^\omega $
there is a
$f:\omega ^\omega \to \omega ^\omega $
there is a
 $g \in A$
so that
$g \in A$
so that
 $\mu (\{x \; | \; f(x)\in ^* g(x)\}) = 1$
.
$\mu (\{x \; | \; f(x)\in ^* g(x)\}) = 1$
.
Let us also recall provable relations for these cardinals. The following diagrams are higher dimensional analogues of Cichoń’s diagram.
Theorem 1.3 [Reference Switzer8, Theorem 1.1].
Interpreting
![]() $\to $
as
$\to $
as
![]() $\leq $
the inequalities shown in Figures 1 and 2 are all provable in
$\leq $
the inequalities shown in Figures 1 and 2 are all provable in
![]() $\mathsf {ZFC}$
.
$\mathsf {ZFC}$
.
We also get the following bounds on these cardinals in terms of
![]() $\omega $
.
$\omega $
.
Lemma 1.4 [Reference Switzer8, Proposition 3.1].
Let
![]() $R \in \{\in ^*, \leq ^*, \neq ^*\}$
and
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
and
![]() $\mathcal I \in \{\mathcal K, \mathcal N, \mathcal M\}$
. In
$\mathcal I \in \{\mathcal K, \mathcal N, \mathcal M\}$
. In
![]() $\mathsf {ZFC}$
it’s provable that
$\mathsf {ZFC}$
it’s provable that
![]() $\mathfrak b(R) \leq \mathfrak b(R_{\mathcal I}) \leq \mathfrak b(R)^{{\textrm {non}}(\mathcal I)}$
.
$\mathfrak b(R) \leq \mathfrak b(R_{\mathcal I}) \leq \mathfrak b(R)^{{\textrm {non}}(\mathcal I)}$
.
It was previously left open whether these cardinals could be less than the continuum. We answer this in the affirmative for the
![]() $\mathfrak b(R_{\mathcal I})$
cardinals and in the negative for the
$\mathfrak b(R_{\mathcal I})$
cardinals and in the negative for the
![]() $\mathfrak {d} (R_{\mathcal I})$
cardinals. In the case of the
$\mathfrak {d} (R_{\mathcal I})$
cardinals. In the case of the
![]() $\mathfrak b(R_{\mathcal I})$
cardinals this is a consequence of the following theorem.
$\mathfrak b(R_{\mathcal I})$
cardinals this is a consequence of the following theorem.
Main Theorem 1.1. Suppose
![]() $R, S \in \{\in ^*, \leq ^*, \neq ^*\}$
and
$R, S \in \{\in ^*, \leq ^*, \neq ^*\}$
and
![]() $\mathcal I, \mathcal J \in \{\mathcal K, \mathcal N, \mathcal M\}$
. With one exception, if
$\mathcal I, \mathcal J \in \{\mathcal K, \mathcal N, \mathcal M\}$
. With one exception, if
![]() $\mathfrak {b}(R_{\mathcal I}) \leq \mathfrak {b}(S_{\mathcal J})$
is not an inequality in either of Figures 1 and 2 then it is consistently false. Moreover, for every R and
$\mathfrak {b}(R_{\mathcal I}) \leq \mathfrak {b}(S_{\mathcal J})$
is not an inequality in either of Figures 1 and 2 then it is consistently false. Moreover, for every R and
![]() $\mathcal I$
,
$\mathcal I$
,
![]() $\mathfrak b(R_{\mathcal I})$
can be strictly less than the continuum. More succinctly, with one possible exception, there are no
$\mathfrak b(R_{\mathcal I})$
can be strictly less than the continuum. More succinctly, with one possible exception, there are no
![]() $\mathsf {ZFC}$
provable inequalities between the cardinals
$\mathsf {ZFC}$
provable inequalities between the cardinals
![]() $\mathfrak b(R_{\mathcal I})$
beyond what is stated in Theorem 1.3 and Lemma 1.4.
$\mathfrak b(R_{\mathcal I})$
beyond what is stated in Theorem 1.3 and Lemma 1.4.
The exception is that
![]() $\mathfrak{b}(\in^*_{\mathcal K}) \leq \mathfrak{b}(\neq^*_{\mathcal N})$
holds in
$\mathfrak{b}(\in^*_{\mathcal K}) \leq \mathfrak{b}(\neq^*_{\mathcal N})$
holds in
![]() $\mathsf{ZFC}$
, as shown recently by the first author (unpublished).This is discussed below, see Question 1 in Section 7.
$\mathsf{ZFC}$
, as shown recently by the first author (unpublished).This is discussed below, see Question 1 in Section 7.

Figure 1 Higher dimensional cardinal characteristics mod the null ideal.

Figure 2 Higher dimensional cardinal characteristics mod the meager and
![]() $\sigma $
-compact ideals.
$\sigma $
-compact ideals.
Main Theorem 1.1 follows cumulatively from the analysis of the various models in Section 4. The second main theorem is the following, due to the first author.
Main Theorem 1.2. Assume
![]() $\mathsf {CH}$
. For all
$\mathsf {CH}$
. For all
![]() $R \in \{\in ^*, \leq ^*, \neq ^*\}$
and all
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
and all
![]() $\,\mathcal {I} \in \{\mathcal K, \mathcal M, \mathcal N\}$
we have
$\,\mathcal {I} \in \{\mathcal K, \mathcal M, \mathcal N\}$
we have
![]() $\mathfrak b(R_{\mathcal I}) = \mathfrak b_{\aleph _1}$
and
$\mathfrak b(R_{\mathcal I}) = \mathfrak b_{\aleph _1}$
and
![]() $\mathfrak {d}(R_{\mathcal I}) = \mathfrak {d}_{\aleph _1}$
.
$\mathfrak {d}(R_{\mathcal I}) = \mathfrak {d}_{\aleph _1}$
.
Here,
![]() $\mathfrak b_\kappa $
and
$\mathfrak b_\kappa $
and
![]() $\mathfrak {d}_\kappa $
are the generalized bounding and dominating numbers for the eventual domination relation on a given cardinal
$\mathfrak {d}_\kappa $
are the generalized bounding and dominating numbers for the eventual domination relation on a given cardinal
![]() $\kappa $
. Main Theorem 1.2 addresses a number of questions left open about the models constructed in Section 4 of [Reference Switzer8]. There, consistent inequalities between the cardinals in Figures 1 and 2 were constructed under
$\kappa $
. Main Theorem 1.2 addresses a number of questions left open about the models constructed in Section 4 of [Reference Switzer8]. There, consistent inequalities between the cardinals in Figures 1 and 2 were constructed under
![]() $\mathsf {CH}$
. From this theorem we see that, in fact, there was an easier way to obtain those results.
$\mathsf {CH}$
. From this theorem we see that, in fact, there was an easier way to obtain those results.
We also study the cardinals
![]() $\mathfrak {d}(R_{\mathcal I})$
when
$\mathfrak {d}(R_{\mathcal I})$
when
![]() $\mathsf {CH}$
fails and show that the above Main Theorem 1.2 can fail in this context.
$\mathsf {CH}$
fails and show that the above Main Theorem 1.2 can fail in this context.
Main Theorem 1.3. For all
![]() $\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
it is consistent that
$\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
it is consistent that
![]() $\mathfrak {d}(\leq ^*_{\mathcal I})< \mathfrak {d}(\in ^*_{\mathcal I})$
and
$\mathfrak {d}(\leq ^*_{\mathcal I})< \mathfrak {d}(\in ^*_{\mathcal I})$
and
![]() $\mathfrak {d} (\neq ^*_{\mathcal I})< \mathfrak {d}(\leq ^*_{\mathcal I})$
.
$\mathfrak {d} (\neq ^*_{\mathcal I})< \mathfrak {d}(\leq ^*_{\mathcal I})$
.
However, surprisingly, the ideal does not matter for the
![]() $\mathfrak {d}(R_{\mathcal I})$
cardinals (in contrast to the
$\mathfrak {d}(R_{\mathcal I})$
cardinals (in contrast to the
![]() $\mathfrak b(R_{\mathcal I})$
cardinals), a result also due to the first author.
$\mathfrak b(R_{\mathcal I})$
cardinals), a result also due to the first author.
Main Theorem 1.4. For all
![]() $R \in \{\in ^*, \leq ^*, \neq ^*\}, \mathsf {ZFC}$
proves that
$R \in \{\in ^*, \leq ^*, \neq ^*\}, \mathsf {ZFC}$
proves that
![]() $\mathfrak {d}(R_{\mathcal N}) = \mathfrak {d}(R_{\mathcal M}) = \mathfrak {d} (R_{\mathcal K})$
.
$\mathfrak {d}(R_{\mathcal N}) = \mathfrak {d}(R_{\mathcal M}) = \mathfrak {d} (R_{\mathcal K})$
.
Main Theorems 1.1, 1.3 and 1.4 above taken together show that duality fails strongly for these higher cardinal characteristics, making their theory starkly different from that of the classical cardinal characteristics as studied for example in [Reference Bartoszyński and Judah1] or [Reference Blass, Foreman and Kanamori2] or even their higher dimensional analogues on
![]() $\kappa $
, see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4]. See [Reference Blass, Foreman and Kanamori2, Section 4] for a particular discussion of this point in the context of cardinals on
$\kappa $
, see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4]. See [Reference Blass, Foreman and Kanamori2, Section 4] for a particular discussion of this point in the context of cardinals on
![]() $\omega $
.
$\omega $
.
The rest of this article is organized as follows. In the next section we study the
![]() $\mathsf {CH}$
case, culminating in the proof of Main Theorem 1.2. In Section 3 we prove a number of
$\mathsf {CH}$
case, culminating in the proof of Main Theorem 1.2. In Section 3 we prove a number of
![]() $\mathsf {ZFC}$
results concerning various implications between the higher dimensional bounding numbers, cardinals on
$\mathsf {ZFC}$
results concerning various implications between the higher dimensional bounding numbers, cardinals on
![]() $\omega $
and the continuum. In Section 4 we study the bounding numbers for the relations
$\omega $
and the continuum. In Section 4 we study the bounding numbers for the relations
![]() $R_{\mathcal I}$
in well known models of
$R_{\mathcal I}$
in well known models of
![]() $\neg \mathsf {CH}$
, culminating in a proof of Main Theorem 1.1. In Section 5 we study the
$\neg \mathsf {CH}$
, culminating in a proof of Main Theorem 1.1. In Section 5 we study the
![]() $\mathfrak {d}(R_{\mathcal I})$
cardinals, showing Main Theorem 1.4. In Section 6 we study consistent inequalities between the dominating numbers culminating in the proof of Main Theorem 1.3. Section 7 concludes with some open questions and final remarks.
$\mathfrak {d}(R_{\mathcal I})$
cardinals, showing Main Theorem 1.4. In Section 6 we study consistent inequalities between the dominating numbers culminating in the proof of Main Theorem 1.3. Section 7 concludes with some open questions and final remarks.
2 The
 $\mathsf {CH}$
case and eventual domination in generalized Baire space
$\mathsf {CH}$
case and eventual domination in generalized Baire space
In this section we prove Main Theorem 1.2. In fact we show something slightly stronger, from which Main Theorem 1.2 follows immediately. We show the following.
Theorem 2.1. Assume
![]() $\mathfrak {c} = \mathfrak {c}^{{<}\mathfrak {c}}$
is a successor cardinal. Fix
$\mathfrak {c} = \mathfrak {c}^{{<}\mathfrak {c}}$
is a successor cardinal. Fix
![]() $R \in \{\in ^*, \leq ^*, \neq ^*\}$
and
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
and
![]() $\mathcal I \in \{\mathcal K, \mathcal M, \mathcal N\}$
. If
$\mathcal I \in \{\mathcal K, \mathcal M, \mathcal N\}$
. If
![]() $\mathfrak b(R) = {\mathrm{add}}(\mathcal I) = \mathfrak {c}$
then
$\mathfrak b(R) = {\mathrm{add}}(\mathcal I) = \mathfrak {c}$
then
![]() $\mathfrak b(R_{\mathcal I}) = \mathfrak b_{\mathfrak {c}}$
and
$\mathfrak b(R_{\mathcal I}) = \mathfrak b_{\mathfrak {c}}$
and
![]() $\mathfrak {d}(R_{\mathcal I}) = \mathfrak {d}_{\mathfrak {c}}$
. In particular these equalities hold under
$\mathfrak {d}(R_{\mathcal I}) = \mathfrak {d}_{\mathfrak {c}}$
. In particular these equalities hold under
![]() $\mathsf {CH}$
.
$\mathsf {CH}$
.
Again recall that here, for any
![]() $\kappa $
, that if
$\kappa $
, that if
![]() $f, g \in \kappa ^\kappa $
then
$f, g \in \kappa ^\kappa $
then
![]() $f\leq ^* g$
if
$f\leq ^* g$
if
![]() $\{\alpha \; | \; f(\alpha ) \nleq g(\alpha )\}$
is bounded. The cardinals
$\{\alpha \; | \; f(\alpha ) \nleq g(\alpha )\}$
is bounded. The cardinals
![]() $\mathfrak b_\kappa $
and
$\mathfrak b_\kappa $
and
![]() $\mathfrak {d}_\kappa $
denote the bounding and dominating numbers for this relation respectively.
$\mathfrak {d}_\kappa $
denote the bounding and dominating numbers for this relation respectively.
Of course, in light of Main Theorem 1.4 adding in the ideal
![]() $\mathcal I$
for the dominating numbers is redundant, however we are interested in a duality result for the bounding numbers as well so we leave it in. Towards proving Theorem 2.1 we start with the following lemma.
$\mathcal I$
for the dominating numbers is redundant, however we are interested in a duality result for the bounding numbers as well so we leave it in. Towards proving Theorem 2.1 we start with the following lemma.
Lemma 2.2. Fix
![]() $R \in \{\in ^*, \leq ^*, \neq ^*\}$
and
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
and
![]() $\mathcal I \in \{\mathcal K, \mathcal M, \mathcal N\}$
. If
$\mathcal I \in \{\mathcal K, \mathcal M, \mathcal N\}$
. If
![]() $\mathfrak b(R) = {\mathrm{non}}(\mathcal I) = \mathfrak {c}$
then
$\mathfrak b(R) = {\mathrm{non}}(\mathcal I) = \mathfrak {c}$
then
![]() $\mathfrak {d}(R_{\mathcal I}) \leq \mathfrak {d}_{\mathfrak {c}}$
and
$\mathfrak {d}(R_{\mathcal I}) \leq \mathfrak {d}_{\mathfrak {c}}$
and
![]() $\mathfrak b_{\mathfrak {c}} \leq \mathfrak b(R_{\mathcal I})$
.
$\mathfrak b_{\mathfrak {c}} \leq \mathfrak b(R_{\mathcal I})$
.
Proof Fix R and
![]() $\mathcal I$
as in the statement of the lemma and assume
$\mathcal I$
as in the statement of the lemma and assume
![]() $\mathfrak b(R) = {\textrm {non}}(\mathcal I) = \mathfrak {c}$
. Enumerate
$\mathfrak b(R) = {\textrm {non}}(\mathcal I) = \mathfrak {c}$
. Enumerate
![]() $\omega ^\omega $
as
$\omega ^\omega $
as
![]() $\{x_\alpha \; | \; \alpha < \mathfrak {c}\}$
and for each
$\{x_\alpha \; | \; \alpha < \mathfrak {c}\}$
and for each
![]() $\alpha < \mathfrak {c}$
fix an element
$\alpha < \mathfrak {c}$
fix an element
![]() $y_\alpha $
of
$y_\alpha $
of
![]() $\omega ^\omega $
(or
$\omega ^\omega $
(or
![]() $\mathcal S$
in the case that
$\mathcal S$
in the case that
![]() $R = \in ^*$
) so that for all
$R = \in ^*$
) so that for all
![]() $\beta \leq \alpha $
,
$\beta \leq \alpha $
,
![]() $x_\beta \mathbin{R} y_\alpha $
. Such a
$x_\beta \mathbin{R} y_\alpha $
. Such a
![]() $y_\alpha $
exists by the assumption on
$y_\alpha $
exists by the assumption on
![]() $\mathfrak b(R)$
. Define
$\mathfrak b(R)$
. Define
![]() $\Psi :\mathfrak {c}^{\mathfrak {c}} \to (\omega ^\omega )^{\omega ^\omega }$
by letting
$\Psi :\mathfrak {c}^{\mathfrak {c}} \to (\omega ^\omega )^{\omega ^\omega }$
by letting
![]() $\Psi (f):\omega ^\omega \to \omega ^\omega $
be given by
$\Psi (f):\omega ^\omega \to \omega ^\omega $
be given by
![]() $\Psi (f)(x_\alpha ) = y_{f(\alpha )}$
. Let
$\Psi (f)(x_\alpha ) = y_{f(\alpha )}$
. Let
![]() $D = \{f_\gamma \; | \; \gamma < \mathfrak {d}_{\mathfrak {c}}\} \subseteq \mathfrak {c}^{\mathfrak {c}}$
be a dominating family of minimal size. Now, let
$D = \{f_\gamma \; | \; \gamma < \mathfrak {d}_{\mathfrak {c}}\} \subseteq \mathfrak {c}^{\mathfrak {c}}$
be a dominating family of minimal size. Now, let
![]() $\Psi (D) = \{\Psi (f_\gamma ) \; |\; \gamma < \mathfrak {d}_{\mathfrak {c}}\}$
. We claim that this is a
$\Psi (D) = \{\Psi (f_\gamma ) \; |\; \gamma < \mathfrak {d}_{\mathfrak {c}}\}$
. We claim that this is a
![]() $R_{\mathcal I}$
dominating family. To see this, fix
$R_{\mathcal I}$
dominating family. To see this, fix
![]() $g:\omega ^\omega \to \omega ^\omega $
and consider
$g:\omega ^\omega \to \omega ^\omega $
and consider
![]() $\hat {g}:\mathfrak {c} \to \mathfrak {c}$
given by
$\hat {g}:\mathfrak {c} \to \mathfrak {c}$
given by
![]() $\hat {g}(\alpha ) = \beta $
if and only if
$\hat {g}(\alpha ) = \beta $
if and only if
![]() $g(x_\alpha ) = x_\beta $
. Now there is some
$g(x_\alpha ) = x_\beta $
. Now there is some
![]() $f_\gamma \in D$
which dominates
$f_\gamma \in D$
which dominates
![]() $\hat {g}$
mod
$\hat {g}$
mod
![]() $<{\mathfrak {c}}$
. But then the set of reals
$<{\mathfrak {c}}$
. But then the set of reals
![]() $x \in \omega ^\omega $
for which
$x \in \omega ^\omega $
for which
![]() $\neg g(x) \mathbin{R} \Psi (f_\gamma )(x)$
has size less than
$\neg g(x) \mathbin{R} \Psi (f_\gamma )(x)$
has size less than
![]() $\mathfrak {c}$
and hence, by the assumption on
$\mathfrak {c}$
and hence, by the assumption on
![]() ${\textrm {non}}(\mathcal I)$
we get that
${\textrm {non}}(\mathcal I)$
we get that
![]() $g \mathbin{R_{\mathcal I}} \Psi (f_\gamma )$
as needed.
$g \mathbin{R_{\mathcal I}} \Psi (f_\gamma )$
as needed.
The other inequality is essentially proved by duality. More precisely, suppose
![]() $\kappa < \mathfrak b_{\mathfrak {c}}$
and
$\kappa < \mathfrak b_{\mathfrak {c}}$
and
![]() $A \subseteq (\omega ^\omega )^{\omega ^\omega }$
is a set of functions of size
$A \subseteq (\omega ^\omega )^{\omega ^\omega }$
is a set of functions of size
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\hat {A} = \{\hat {g} \; | \; g \in A\}$
where
$\hat {A} = \{\hat {g} \; | \; g \in A\}$
where
![]() $g \mapsto \hat {g}$
is as defined in the previous paragraph. Since
$g \mapsto \hat {g}$
is as defined in the previous paragraph. Since
![]() $\hat {A}$
has size
$\hat {A}$
has size
![]() $\kappa $
it’s bounded, say by some
$\kappa $
it’s bounded, say by some
![]() $f \in \mathfrak {c}^{\mathfrak {c}}$
. Essentially the same proof as in the previous paragraph then shows
$f \in \mathfrak {c}^{\mathfrak {c}}$
. Essentially the same proof as in the previous paragraph then shows
![]() $\Psi (f)$
is an
$\Psi (f)$
is an
![]() $R_{\mathcal I}$
-bound on A.
$R_{\mathcal I}$
-bound on A.
Lemma 2.3. Fix
![]() $R \in \{\in ^*, \leq ^*, \neq ^*\}$
and
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
and
![]() $\mathcal I \in \{\mathcal K, \mathcal M, \mathcal N\}$
. If
$\mathcal I \in \{\mathcal K, \mathcal M, \mathcal N\}$
. If
![]() ${\mathrm{add}}(\mathcal I) = \mathfrak {c}$
then
${\mathrm{add}}(\mathcal I) = \mathfrak {c}$
then
![]() $\mathfrak {d}_{\mathfrak {c}} (\neq ^*) \leq \mathfrak {d}(R_{\mathcal I})$
and
$\mathfrak {d}_{\mathfrak {c}} (\neq ^*) \leq \mathfrak {d}(R_{\mathcal I})$
and
![]() $\mathfrak b(R_{\mathcal I}) \leq \mathfrak b_{\mathfrak {c}}(\neq ^*)$
.
$\mathfrak b(R_{\mathcal I}) \leq \mathfrak b_{\mathfrak {c}}(\neq ^*)$
.
Here recall that if
![]() $f, g \in \kappa ^\kappa $
then
$f, g \in \kappa ^\kappa $
then
![]() $f\neq ^* g$
if the set of
$f\neq ^* g$
if the set of
![]() $\alpha $
for which
$\alpha $
for which
![]() $f(\alpha ) = g(\alpha )$
has size less than
$f(\alpha ) = g(\alpha )$
has size less than
![]() $\kappa $
. The bounding and dominating numbers for this relation are denoted respectively
$\kappa $
. The bounding and dominating numbers for this relation are denoted respectively
![]() $\mathfrak b_\kappa (\neq ^*)$
and
$\mathfrak b_\kappa (\neq ^*)$
and
![]() $\mathfrak {d}_\kappa (\neq ^*)$
, see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Definition 16].
$\mathfrak {d}_\kappa (\neq ^*)$
, see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Definition 16].
Proof Fix R and
![]() $\mathcal I$
as in the statement of the lemma and assume
$\mathcal I$
as in the statement of the lemma and assume
![]() ${\textrm {add}}(\mathcal I) = \mathfrak {c}$
. We show that
${\textrm {add}}(\mathcal I) = \mathfrak {c}$
. We show that
![]() $\mathfrak {d}_{\mathfrak {c}} (\neq ^*) \leq \mathfrak {d}(\neq ^*_{\mathcal I})$
. Let
$\mathfrak {d}_{\mathfrak {c}} (\neq ^*) \leq \mathfrak {d}(\neq ^*_{\mathcal I})$
. Let
![]() $\{A_\gamma \; | \; \gamma < \mathfrak {c}\}$
be an increasing, cofinal family of sets from
$\{A_\gamma \; | \; \gamma < \mathfrak {c}\}$
be an increasing, cofinal family of sets from
![]() $\mathcal I$
(that such a family exists follows from
$\mathcal I$
(that such a family exists follows from
![]() ${\textrm {add}}(\mathcal I) = \mathfrak {c}$
). Choose
${\textrm {add}}(\mathcal I) = \mathfrak {c}$
). Choose
![]() $\{x_\gamma \; | \; \gamma < \mathfrak {c}\} \subseteq \omega ^\omega $
so that for all
$\{x_\gamma \; | \; \gamma < \mathfrak {c}\} \subseteq \omega ^\omega $
so that for all
![]() $\gamma < \mathfrak {c}$
we have
$\gamma < \mathfrak {c}$
we have
![]() $x_\gamma \notin A_\gamma $
. Now fix an
$x_\gamma \notin A_\gamma $
. Now fix an
![]() $\neq ^*_{\mathcal I}$
-dominating family
$\neq ^*_{\mathcal I}$
-dominating family
![]() $\mathcal F = \{f_\alpha \; | \; \alpha < \mathfrak {d}(\neq ^*_{\mathcal I}) \}$
. Let
$\mathcal F = \{f_\alpha \; | \; \alpha < \mathfrak {d}(\neq ^*_{\mathcal I}) \}$
. Let
![]() $F:\mathfrak {c} \to \omega ^\omega $
be a bijection. Define
$F:\mathfrak {c} \to \omega ^\omega $
be a bijection. Define
![]() $g_\alpha : \mathfrak {c} \to \mathfrak {c}$
by
$g_\alpha : \mathfrak {c} \to \mathfrak {c}$
by
![]() $g_\alpha (\gamma ) = F^{-1}(f_\alpha (x_\gamma ))$
. We claim that
$g_\alpha (\gamma ) = F^{-1}(f_\alpha (x_\gamma ))$
. We claim that
![]() $\{g_\alpha \; | \; \alpha < \mathfrak {d}(\neq ^*_{\mathcal I})\}$
is a dominating family for the relation
$\{g_\alpha \; | \; \alpha < \mathfrak {d}(\neq ^*_{\mathcal I})\}$
is a dominating family for the relation
![]() $\neq ^*$
on
$\neq ^*$
on
![]() $\mathfrak {c}^{\mathfrak {c}}$
. Indeed suppose that
$\mathfrak {c}^{\mathfrak {c}}$
. Indeed suppose that
![]() $g:\mathfrak {c} \to \mathfrak {c}$
is arbitrary. Let
$g:\mathfrak {c} \to \mathfrak {c}$
is arbitrary. Let
![]() $f:\omega ^\omega \to \omega ^\omega $
be such that
$f:\omega ^\omega \to \omega ^\omega $
be such that
![]() $f(x_\gamma ) = F(g(\gamma ))$
(the other values of f are irrelevant). By assumption we know that for some
$f(x_\gamma ) = F(g(\gamma ))$
(the other values of f are irrelevant). By assumption we know that for some
![]() $\alpha < \mathfrak {d}(\neq ^*_{\mathcal I})$
the set
$\alpha < \mathfrak {d}(\neq ^*_{\mathcal I})$
the set
![]() $\{x \; | \; \exists ^\infty n \, f(x)(n) = f_\alpha (x)(n)\}$
is in
$\{x \; | \; \exists ^\infty n \, f(x)(n) = f_\alpha (x)(n)\}$
is in
![]() ${\mathcal I}$
and so it lies in some
${\mathcal I}$
and so it lies in some
![]() $A_\gamma $
. As a result for all but
$A_\gamma $
. As a result for all but
![]() ${<}\mathfrak {c}$
many
${<}\mathfrak {c}$
many
![]() $\gamma $
we have that
$\gamma $
we have that
![]() $F(g(\gamma )) = f(x_\gamma ) \neq ^* f_\alpha (x_\gamma ) = F(g_\alpha (\gamma ))$
and thus
$F(g(\gamma )) = f(x_\gamma ) \neq ^* f_\alpha (x_\gamma ) = F(g_\alpha (\gamma ))$
and thus
![]() $g(\gamma ) \neq g_\alpha (\gamma )$
for all but
$g(\gamma ) \neq g_\alpha (\gamma )$
for all but
![]() ${<}\mathfrak {c}$
many
${<}\mathfrak {c}$
many
![]() $\gamma $
as needed.
$\gamma $
as needed.
The proof for the bounding numbers is dual to the one above. The details are left to the reader.
Putting together Lemmas 2.2 and 2.3 alongside the fact that if
![]() $\kappa $
is a successor cardinal for which
$\kappa $
is a successor cardinal for which
![]() $\kappa ^{<\kappa } = \kappa $
then
$\kappa ^{<\kappa } = \kappa $
then
![]() $\mathfrak b_\kappa (\neq ^*) = \mathfrak b_\kappa $
and
$\mathfrak b_\kappa (\neq ^*) = \mathfrak b_\kappa $
and
![]() $\mathfrak {d}_\kappa (\neq ^*) = \mathfrak {d}_\kappa $
, see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Theorem 21], now implies Theorem 2.1.
$\mathfrak {d}_\kappa (\neq ^*) = \mathfrak {d}_\kappa $
, see [Reference Brendle, Brooke-Taylor, Friedman and Montoya4, Theorem 21], now implies Theorem 2.1.
3
 $\mathsf {ZFC}$
results for the bounding numbers
$\mathsf {ZFC}$
results for the bounding numbers
We begin by giving a number of
![]() $\mathsf {ZFC}$
results about the higher dimensional cardinals of the form
$\mathsf {ZFC}$
results about the higher dimensional cardinals of the form
![]() $\mathfrak b(R_{\mathcal I})$
and their counterparts on
$\mathfrak b(R_{\mathcal I})$
and their counterparts on
![]() $\omega $
that will be used to prove Main Theorem 1.1. The first lemma was originally proved in [Reference Switzer8, Lemma 3.2]. The proof is simply a standard diagonal argument, making use of the assumptions.
$\omega $
that will be used to prove Main Theorem 1.1. The first lemma was originally proved in [Reference Switzer8, Lemma 3.2]. The proof is simply a standard diagonal argument, making use of the assumptions.
Lemma 3.1 [Reference Switzer8, Lemma 3.2].
For each
![]() $\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
and
$\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
and
![]() $R \in \{ \in ^*, \leq ^*, \neq ^*\}$
, if
$R \in \{ \in ^*, \leq ^*, \neq ^*\}$
, if
![]() $\mathfrak {b}(R) = {\mathrm{non}} (\mathcal I) = \mathfrak {c}$
then
$\mathfrak {b}(R) = {\mathrm{non}} (\mathcal I) = \mathfrak {c}$
then
![]() $\mathfrak {c}^+ \leq \mathfrak {b}(R_{\mathcal I})$
.
$\mathfrak {c}^+ \leq \mathfrak {b}(R_{\mathcal I})$
.
This lemma is actually strengthened by Lemma 2.2, however this is the version we will need in Section 4 so we quote it here. The next two lemmas show how relations between the cardinals on R and
![]() $\mathcal I$
can have consequences for the value of
$\mathcal I$
can have consequences for the value of
![]() $\mathfrak b(R_{\mathcal I})$
.
$\mathfrak b(R_{\mathcal I})$
.
Lemma 3.2. Suppose
![]() $\mathfrak b (R) < {\mathrm{cov}}(\mathcal I)$
. Then
$\mathfrak b (R) < {\mathrm{cov}}(\mathcal I)$
. Then
![]() $\mathfrak b (R_{\mathcal I}) = \mathfrak b (R)$
.
$\mathfrak b (R_{\mathcal I}) = \mathfrak b (R)$
.
Proof By Lemma 1.4 it suffices to prove that under the hypothesis
![]() $\mathfrak b(R_{\mathcal I}) \leq \mathfrak b(R)$
. Let
$\mathfrak b(R_{\mathcal I}) \leq \mathfrak b(R)$
. Let
![]() $A = \{x_\alpha \; | \; \alpha < \mathfrak b(R)\}$
be an R-unbounded family of minimal size and for each
$A = \{x_\alpha \; | \; \alpha < \mathfrak b(R)\}$
be an R-unbounded family of minimal size and for each
![]() $\alpha < \mathfrak b(R)$
let
$\alpha < \mathfrak b(R)$
let
![]() $c_\alpha :\omega ^\omega \to \omega ^\omega $
be the constant function with value
$c_\alpha :\omega ^\omega \to \omega ^\omega $
be the constant function with value
![]() $x_\alpha $
. We claim that the family
$x_\alpha $
. We claim that the family
![]() $\{c_\alpha \; | \; \alpha < \mathfrak b(R)\}$
forms an
$\{c_\alpha \; | \; \alpha < \mathfrak b(R)\}$
forms an
![]() $R_{\mathcal I}$
-unbounded family. To see this, suppose that
$R_{\mathcal I}$
-unbounded family. To see this, suppose that
![]() $f:\omega ^\omega \to \omega ^\omega $
(or
$f:\omega ^\omega \to \omega ^\omega $
(or
![]() $f:\omega ^\omega \to \mathcal S$
) were a bound. Define a function
$f:\omega ^\omega \to \mathcal S$
) were a bound. Define a function
![]() $h \in (\omega ^\omega )^{\omega ^\omega }$
so that for each
$h \in (\omega ^\omega )^{\omega ^\omega }$
so that for each
![]() $x\in \omega ^\omega $
let
$x\in \omega ^\omega $
let
![]() $h(x) \in A$
be R-unbounded by
$h(x) \in A$
be R-unbounded by
![]() $f(x)$
. Since no family of sets in
$f(x)$
. Since no family of sets in
![]() $\mathcal I$
of size
$\mathcal I$
of size
![]() $\mathfrak b(R)$
is covering, there must be some
$\mathfrak b(R)$
is covering, there must be some
![]() $x_\alpha \in A$
so that
$x_\alpha \in A$
so that
![]() $h^{-1}(\{x_\alpha \})$
is not in
$h^{-1}(\{x_\alpha \})$
is not in
![]() $\mathcal I$
. But this means that on a non-
$\mathcal I$
. But this means that on a non-
![]() $\mathcal I$
set
$\mathcal I$
set
![]() $c_\alpha $
is not bounded by f, so f is not a bound on
$c_\alpha $
is not bounded by f, so f is not a bound on
![]() $\{c_\alpha \; | \; \alpha < \mathfrak b(R)\}$
as needed.
$\{c_\alpha \; | \; \alpha < \mathfrak b(R)\}$
as needed.
Lemma 3.3. If
![]() ${\textrm {cov}} (\mathcal I) = \aleph _1$
then
${\textrm {cov}} (\mathcal I) = \aleph _1$
then
![]() $\mathfrak b (\in ^*_{\mathcal I}) \geq \aleph _2$
.
$\mathfrak b (\in ^*_{\mathcal I}) \geq \aleph _2$
.
Proof Fix a family
![]() $\{A_\alpha \; | \; \alpha < \aleph _1\}$
of sets from
$\{A_\alpha \; | \; \alpha < \aleph _1\}$
of sets from
![]() $\mathcal I$
covering
$\mathcal I$
covering
![]() $\omega ^\omega $
. Without loss, assume that they are disjoint. Let
$\omega ^\omega $
. Without loss, assume that they are disjoint. Let
![]() $\{f_\alpha \; | \; \alpha < \aleph _1\}$
be a family of functions
$\{f_\alpha \; | \; \alpha < \aleph _1\}$
be a family of functions
![]() $f_\alpha : \omega ^\omega \to \omega ^\omega $
. We need to provide a bound
$f_\alpha : \omega ^\omega \to \omega ^\omega $
. We need to provide a bound
![]() $g:\omega ^\omega \to \mathcal S$
. We can do this by defining for
$g:\omega ^\omega \to \mathcal S$
. We can do this by defining for
![]() $x \in A_\alpha $
,
$x \in A_\alpha $
,
![]() $g(x)$
to be any slalom bounding the countable set
$g(x)$
to be any slalom bounding the countable set
![]() $\{f_\beta (x) \; | \; \beta < \alpha \}$
. Now, suppose that
$\{f_\beta (x) \; | \; \beta < \alpha \}$
. Now, suppose that
![]() $\alpha < \omega _1$
and observe that for all
$\alpha < \omega _1$
and observe that for all
![]() $x \notin \bigcup _{\beta \leq \alpha } A_\beta $
we have that
$x \notin \bigcup _{\beta \leq \alpha } A_\beta $
we have that
![]() $f_\alpha (x) \in ^* g(x)$
and since the latter is in
$f_\alpha (x) \in ^* g(x)$
and since the latter is in
![]() $\mathcal I$
(since it’s a countable union), we’re done.
$\mathcal I$
(since it’s a countable union), we’re done.
A surprising corollary of this result is the following.
Proposition 3.4.
![]() $\mathfrak b (\neq ^*_{\mathcal N}) \geq \aleph _2$
.
$\mathfrak b (\neq ^*_{\mathcal N}) \geq \aleph _2$
.
Proof If
![]() ${\textrm {cov}}(\mathcal N) = \aleph _1$
then the result follows from Lemma 3.3 plus the fact that
${\textrm {cov}}(\mathcal N) = \aleph _1$
then the result follows from Lemma 3.3 plus the fact that
![]() $\mathfrak b(\in ^*_{\mathcal N}) \leq \mathfrak b(\neq ^*_{\mathcal N})$
. Otherwise
$\mathfrak b(\in ^*_{\mathcal N}) \leq \mathfrak b(\neq ^*_{\mathcal N})$
. Otherwise
![]() ${\textrm {cov}}(\mathcal N)> \aleph _1$
. Since
${\textrm {cov}}(\mathcal N)> \aleph _1$
. Since
![]() ${\textrm {cov}}(\mathcal N) \leq \mathfrak b (\neq ^*) = {\textrm {non}}(\mathcal M)$
(in
${\textrm {cov}}(\mathcal N) \leq \mathfrak b (\neq ^*) = {\textrm {non}}(\mathcal M)$
(in
![]() $\mathsf {ZFC}$
) we get that
$\mathsf {ZFC}$
) we get that
![]() $\aleph _2 \leq \mathfrak b(\neq ^*) \leq \mathfrak b(\neq ^*_{\mathcal N})$
.
$\aleph _2 \leq \mathfrak b(\neq ^*) \leq \mathfrak b(\neq ^*_{\mathcal N})$
.
Oddly enough the other eight numbers of the form
![]() $\mathfrak b(R_{\mathcal I})$
can all be
$\mathfrak b(R_{\mathcal I})$
can all be
![]() $\aleph _1$
as we will see. Lemmas 3.1 and 3.3 are both actually special cases of a more general lemma which we prove now.
$\aleph _1$
as we will see. Lemmas 3.1 and 3.3 are both actually special cases of a more general lemma which we prove now.
Lemma 3.5. Fix a cardinal
![]() $\kappa $
and assume that there is a family
$\kappa $
and assume that there is a family
![]() $\mathcal X = \{X_\alpha \; | \; \alpha < \kappa \} \subseteq \mathcal I$
so that for all
$\mathcal X = \{X_\alpha \; | \; \alpha < \kappa \} \subseteq \mathcal I$
so that for all
![]() $\mathcal Y \subseteq \mathcal X$
if
$\mathcal Y \subseteq \mathcal X$
if
![]() $|\mathcal Y| = \mathfrak b(R)$
then
$|\mathcal Y| = \mathfrak b(R)$
then
![]() $\bigcup \mathcal Y = \omega ^\omega $
(i.e.,
$\bigcup \mathcal Y = \omega ^\omega $
(i.e.,
![]() $\mathcal Y$
is covering). Then
$\mathcal Y$
is covering). Then
![]() $\mathfrak b(R_{\mathcal I})> \kappa $
.
$\mathfrak b(R_{\mathcal I})> \kappa $
.
Proof Fix R,
![]() $\mathcal I$
and
$\mathcal I$
and
![]() $\kappa $
and assume there is a family
$\kappa $
and assume there is a family
![]() $\mathcal X = \{X_\alpha \; |\; \alpha < \kappa \}$
as in the statement of the lemma. We need to show that no family of functions
$\mathcal X = \{X_\alpha \; |\; \alpha < \kappa \}$
as in the statement of the lemma. We need to show that no family of functions
![]() $\{f_\alpha \; | \; \alpha < \kappa \} \subseteq (\omega ^\omega )^{\omega ^\omega }$
is
$\{f_\alpha \; | \; \alpha < \kappa \} \subseteq (\omega ^\omega )^{\omega ^\omega }$
is
![]() $R_{\mathcal I}$
-unbounded. Fix such a family. We will define a bound on it. First notice that for each
$R_{\mathcal I}$
-unbounded. Fix such a family. We will define a bound on it. First notice that for each
![]() $x \in \omega ^\omega $
the set
$x \in \omega ^\omega $
the set
![]() $\{\gamma \; | \; x \notin X_\gamma \}$
has size
$\{\gamma \; | \; x \notin X_\gamma \}$
has size
![]() ${<}\mathfrak b(R)$
since every family of size
${<}\mathfrak b(R)$
since every family of size
![]() $\mathfrak b(R)$
is covering. Now define
$\mathfrak b(R)$
is covering. Now define
![]() $g:\omega ^\omega \to \omega ^\omega $
so that for all
$g:\omega ^\omega \to \omega ^\omega $
so that for all
![]() $x \in \omega ^\omega $
we have
$x \in \omega ^\omega $
we have
![]() $g(x)$
is an R-bound on
$g(x)$
is an R-bound on
![]() $\{f_\gamma (x) \; | \; x \notin X_\gamma \}$
. We claim that this
$\{f_\gamma (x) \; | \; x \notin X_\gamma \}$
. We claim that this
![]() $g\ R_{\mathcal I}$
-dominates every
$g\ R_{\mathcal I}$
-dominates every
![]() $f_\alpha $
. To see this, fix
$f_\alpha $
. To see this, fix
![]() $\alpha < \kappa $
and consider the set of x so that
$\alpha < \kappa $
and consider the set of x so that
![]() $\neg ( f_\alpha (x) \mathbin{R} g(x) )$
. If x is in this set, then by the definition of g we have that
$\neg ( f_\alpha (x) \mathbin{R} g(x) )$
. If x is in this set, then by the definition of g we have that
![]() $x \in X_\alpha $
. Since this later set is in
$x \in X_\alpha $
. Since this later set is in
![]() $\mathcal I$
this completes the proof.
$\mathcal I$
this completes the proof.
Every computation of a
![]() $\mathfrak b(R_{\mathcal I})$
cardinal in this paper (and in [Reference Switzer8]) factors through one of Lemmas 3.1, 3.3 or 3.5. Since the later generalizes the former two, every model in which a cardinal of the form
$\mathfrak b(R_{\mathcal I})$
cardinal in this paper (and in [Reference Switzer8]) factors through one of Lemmas 3.1, 3.3 or 3.5. Since the later generalizes the former two, every model in which a cardinal of the form
![]() $\mathfrak b(R_{\mathcal I})$
is greater than
$\mathfrak b(R_{\mathcal I})$
is greater than
![]() $\mathfrak {c}$
satisfies the hypothesis of Lemma 3.5 with
$\mathfrak {c}$
satisfies the hypothesis of Lemma 3.5 with
![]() $\kappa $
at least the size of the continuum. We do not know if this is necessary or not. Families of sets
$\kappa $
at least the size of the continuum. We do not know if this is necessary or not. Families of sets
![]() $\mathcal X$
as described in Lemma 3.5 are called
$\mathcal X$
as described in Lemma 3.5 are called
![]() $(\kappa , \lambda )$
-Rothberger families for
$(\kappa , \lambda )$
-Rothberger families for
![]() $\mathcal I$
where
$\mathcal I$
where
![]() $\kappa $
is the cardinality of
$\kappa $
is the cardinality of
![]() $\mathcal X$
and
$\mathcal X$
and
![]() $\lambda $
is so that every subfamily of
$\lambda $
is so that every subfamily of
![]() $\mathcal X$
of size
$\mathcal X$
of size
![]() $\lambda $
is covering. In this terminology, Lemma 3.5 can be rephrased as saying that the existence of a
$\lambda $
is covering. In this terminology, Lemma 3.5 can be rephrased as saying that the existence of a
![]() $(\kappa , \mathfrak b(R))$
-Rothberger family for
$(\kappa , \mathfrak b(R))$
-Rothberger family for
![]() $\mathcal I$
implies that
$\mathcal I$
implies that
![]() $\mathfrak b(R_{\mathcal I})> \kappa $
. Such families were investigated in [Reference Cichoń5], see in particular Definition 2.2. In connection with this, note that the case where
$\mathfrak b(R_{\mathcal I})> \kappa $
. Such families were investigated in [Reference Cichoń5], see in particular Definition 2.2. In connection with this, note that the case where
![]() $\kappa < \mathfrak b(R)$
holds vacuously (both the antecedent and the conclusion) so the interesting case is when
$\kappa < \mathfrak b(R)$
holds vacuously (both the antecedent and the conclusion) so the interesting case is when
![]() $\kappa $
is at least
$\kappa $
is at least
![]() $\mathfrak b(R)$
. In this case we obviously have
$\mathfrak b(R)$
. In this case we obviously have
![]() ${\textrm {cov}}(\mathcal I) \leq \mathfrak b(R)$
yet this is not sufficient as, e.g.,
${\textrm {cov}}(\mathcal I) \leq \mathfrak b(R)$
yet this is not sufficient as, e.g.,
![]() ${\textrm {cov}}(\mathcal N) = \mathfrak b(\neq ^*) = 2^{\aleph _0}$
in the random model but given any family of continuum many null sets we can easily find a subfamily also of size continuum and a random real which escapes all of them. Indeed, we will see in Theorem 4.3 that
${\textrm {cov}}(\mathcal N) = \mathfrak b(\neq ^*) = 2^{\aleph _0}$
in the random model but given any family of continuum many null sets we can easily find a subfamily also of size continuum and a random real which escapes all of them. Indeed, we will see in Theorem 4.3 that
![]() $\mathfrak b(\neq ^*_{\mathcal N}) = 2^{\aleph _0}$
so the conclusion of the lemma above is not simply implied by
$\mathfrak b(\neq ^*_{\mathcal N}) = 2^{\aleph _0}$
so the conclusion of the lemma above is not simply implied by
![]() ${\textrm {cov}}(\mathcal I) \leq \mathfrak b(R)$
even. Nevertheless, replacing the null ideal by the meager ideal, such a family does exist in the random model and this is what is used to compute the cardinals
${\textrm {cov}}(\mathcal I) \leq \mathfrak b(R)$
even. Nevertheless, replacing the null ideal by the meager ideal, such a family does exist in the random model and this is what is used to compute the cardinals
![]() $\mathfrak b(\in _{\mathcal M})$
,
$\mathfrak b(\in _{\mathcal M})$
,
![]() $\mathfrak b(\leq ^*_{\mathcal M})$
and
$\mathfrak b(\leq ^*_{\mathcal M})$
and
![]() $\mathfrak b(\neq ^*_{\mathcal M})$
in the random model in Section 4.
$\mathfrak b(\neq ^*_{\mathcal M})$
in the random model in Section 4.
4 Consistency results for the bounding numbers
In this section we study the values of the bounding numbers in Figures 1 and 2 in various classical models of set theory such as the Cohen, random and Sacks models. The basic plan is this: we will iterate some well known forcing over a model of
![]() $\mathsf {GCH}$
to get a model where
$\mathsf {GCH}$
to get a model where
![]() $\mathfrak {c}$
is some specified
$\mathfrak {c}$
is some specified
![]() $\kappa $
and
$\kappa $
and
![]() $2^{\mathfrak {c}} = \mathfrak {c}^+$
. It will follow from Corollary 5.2, which states that
$2^{\mathfrak {c}} = \mathfrak {c}^+$
. It will follow from Corollary 5.2, which states that
![]() $\mathfrak {d}(R_{\mathcal I})> 2^{\aleph _0}$
for all R and
$\mathfrak {d}(R_{\mathcal I})> 2^{\aleph _0}$
for all R and
![]() $\mathcal I$
, that in each model all of the
$\mathcal I$
, that in each model all of the
![]() $\mathfrak {d} (R_{\mathcal I})$
cardinals will be
$\mathfrak {d} (R_{\mathcal I})$
cardinals will be
![]() $\mathfrak {c}^+$
so we focus on the
$\mathfrak {c}^+$
so we focus on the
![]() $\mathfrak b (R_{\mathcal I})$
cardinals. From now on let us fix an arbitrary regular cardinal
$\mathfrak b (R_{\mathcal I})$
cardinals. From now on let us fix an arbitrary regular cardinal
![]() $\kappa> \aleph _1$
. We will need one forcing theoretic lemma.
$\kappa> \aleph _1$
. We will need one forcing theoretic lemma.
Lemma 4.1. Assume
![]() $\mathsf {GCH}$
and suppose
$\mathsf {GCH}$
and suppose
![]() $\mathbb P$
is a finite support or countable support product of proper forcing notions so that if
$\mathbb P$
is a finite support or countable support product of proper forcing notions so that if
![]() $G \subseteq \mathbb P$
is V-generic then in
$G \subseteq \mathbb P$
is V-generic then in
![]() $V[G]$
the reals of V are
$V[G]$
the reals of V are
![]() $\mathcal I$
positive and R-unbounded and the set of Borel codes for elements of
$\mathcal I$
positive and R-unbounded and the set of Borel codes for elements of
![]() $\mathcal I$
in V form a Borel basis for
$\mathcal I$
in V form a Borel basis for
![]() $\mathcal I$
in
$\mathcal I$
in
![]() $V[G]$
when reinterpreted. Then the set of functions
$V[G]$
when reinterpreted. Then the set of functions
![]() $f \in (\omega ^\omega )^{\omega ^\omega } \cap V$
extended arbitrarily to the new reals form an
$f \in (\omega ^\omega )^{\omega ^\omega } \cap V$
extended arbitrarily to the new reals form an
![]() $R_{\mathcal I}$
-unbounded family. In particular,
$R_{\mathcal I}$
-unbounded family. In particular,
![]() $\Vdash _{\mathbb P} \mathfrak b (R_{\mathcal I}) \leq \aleph _2$
.
$\Vdash _{\mathbb P} \mathfrak b (R_{\mathcal I}) \leq \aleph _2$
.
Proof Let
![]() $\{g_\alpha \; | \; \alpha < \aleph _2\}$
be any set of functions so that the set of restrictions to
$\{g_\alpha \; | \; \alpha < \aleph _2\}$
be any set of functions so that the set of restrictions to
![]() $V \cap \omega ^\omega $
is exactly the functions in
$V \cap \omega ^\omega $
is exactly the functions in
![]() $V \cap (\omega ^\omega )^{\omega ^\omega }$
. We need to show that this set is unbounded. Fix a function
$V \cap (\omega ^\omega )^{\omega ^\omega }$
. We need to show that this set is unbounded. Fix a function
![]() $f:\omega ^\omega \to \omega ^\omega $
in
$f:\omega ^\omega \to \omega ^\omega $
in
![]() $V[G]$
. By restricting f to
$V[G]$
. By restricting f to
![]() $V \cap \omega ^\omega $
, the fact that the iteration is a product and
$V \cap \omega ^\omega $
, the fact that the iteration is a product and
![]() $\mathsf {CH}$
holds implies that we can find a set of size
$\mathsf {CH}$
holds implies that we can find a set of size
![]() $\aleph _1$
, say
$\aleph _1$
, say
![]() $X \subseteq \kappa $
so that f is in fact added by the product restricted to this set, call it
$X \subseteq \kappa $
so that f is in fact added by the product restricted to this set, call it
![]() $\mathbb P_X$
, and this forcing has size
$\mathbb P_X$
, and this forcing has size
![]() $\aleph _1$
. Work in V now, and let
$\aleph _1$
. Work in V now, and let
![]() $\dot {f}$
be the name for f. Without loss assume the maximal condition forces
$\dot {f}$
be the name for f. Without loss assume the maximal condition forces
![]() $\dot {f}$
is a function from
$\dot {f}$
is a function from
![]() $\omega ^\omega $
to
$\omega ^\omega $
to
![]() $\omega ^\omega $
. Enumerate Baire space as
$\omega ^\omega $
. Enumerate Baire space as
![]() $\omega ^\omega = \{x_\alpha \; | \; \alpha < \aleph _1\}$
. Also enumerate all pairs
$\omega ^\omega = \{x_\alpha \; | \; \alpha < \aleph _1\}$
. Also enumerate all pairs
![]() $(p_\alpha , B_\alpha )_{\alpha < \omega _1}$
in order type
$(p_\alpha , B_\alpha )_{\alpha < \omega _1}$
in order type
![]() $\omega _1$
of conditions from
$\omega _1$
of conditions from
![]() $\mathbb P_X$
and Borel
$\mathbb P_X$
and Borel
![]() $\mathcal I$
sets coded in V so that
$\mathcal I$
sets coded in V so that
![]() $x_\alpha \notin B_\alpha $
. For each
$x_\alpha \notin B_\alpha $
. For each
![]() $\alpha $
let
$\alpha $
let
![]() $q_\alpha \leq p_\alpha $
decide some ground model real not R-bounded by
$q_\alpha \leq p_\alpha $
decide some ground model real not R-bounded by
![]() $\dot {f} (\check {x}_\alpha )$
. Note that such a real exists in the ground model by assumption. Let (in V)
$\dot {f} (\check {x}_\alpha )$
. Note that such a real exists in the ground model by assumption. Let (in V)
![]() $h \in (\omega ^\omega )^{\omega ^\omega }$
be the function which on
$h \in (\omega ^\omega )^{\omega ^\omega }$
be the function which on
![]() $x_\alpha $
takes the value
$x_\alpha $
takes the value
![]() $q_\alpha $
decides is unbounded by
$q_\alpha $
decides is unbounded by
![]() $\dot {f}$
. We claim that for any
$\dot {f}$
. We claim that for any
![]() $\bar {h}$
in
$\bar {h}$
in
![]() $V[G]$
extending h it’s not the case that
$V[G]$
extending h it’s not the case that
![]() $\bar {h}$
is
$\bar {h}$
is
![]() $R_{\mathcal I}$
-bounded by
$R_{\mathcal I}$
-bounded by
![]() $\dot {f}$
. Indeed, otherwise there is some
$\dot {f}$
. Indeed, otherwise there is some
![]() $\alpha $
so that
$\alpha $
so that
![]() $p_\alpha \Vdash \{x \; | \;\neg \check {h}(x) \mathbin{R} \dot {f}(x)\} \subseteq B_\alpha $
since the Borel sets in
$p_\alpha \Vdash \{x \; | \;\neg \check {h}(x) \mathbin{R} \dot {f}(x)\} \subseteq B_\alpha $
since the Borel sets in
![]() $\mathcal I$
from the ground model form a basis, but
$\mathcal I$
from the ground model form a basis, but
![]() $q_\alpha \leq p_\alpha $
and
$q_\alpha \leq p_\alpha $
and
![]() $q_\alpha $
forces that
$q_\alpha $
forces that
![]() $\neg \check {h}(x_\alpha ) \mathbin{R} \dot {f}(x_\alpha )$
and
$\neg \check {h}(x_\alpha ) \mathbin{R} \dot {f}(x_\alpha )$
and
![]() $x_\alpha \notin B_\alpha $
, which is a contradiction.
$x_\alpha \notin B_\alpha $
, which is a contradiction.
4.1 The Cohen model
The Cohen model is the model obtained by forcing with the finite support product of
![]() $\kappa $
many copies of Cohen forcing over a model of
$\kappa $
many copies of Cohen forcing over a model of
![]() $\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.5.8, p. 386]. We will prove the following theorem.
$\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.5.8, p. 386]. We will prove the following theorem.
Theorem 4.2. In the Cohen model the following equalities hold for all
![]() $R \in \{\in^*, \leq^*, \neq^*\}$
.
$R \in \{\in^*, \leq^*, \neq^*\}$
.
-
(1)
 $\mathfrak b (R_{\mathcal K}) = \mathfrak b (R_{\mathcal M}) = \aleph _1$
$\mathfrak b (R_{\mathcal K}) = \mathfrak b (R_{\mathcal M}) = \aleph _1$
-
(2)
 $\mathfrak b (R_{\mathcal N}) = \kappa ^+$
$\mathfrak b (R_{\mathcal N}) = \kappa ^+$
In words, the numbers associated with
![]() $\mathcal M$
and
$\mathcal M$
and
![]() $\mathcal K$
are
$\mathcal K$
are
![]() $\aleph _1$
and those associated with
$\aleph _1$
and those associated with
![]() $\mathcal N$
are
$\mathcal N$
are
![]() $\kappa ^+$
.
$\kappa ^+$
.
Proof There are two things to show. First that
![]() $\mathfrak b (\in ^*_{\mathcal K}) = \mathfrak b (\neq ^*_{\mathcal M}) = \aleph _1$
and second that
$\mathfrak b (\in ^*_{\mathcal K}) = \mathfrak b (\neq ^*_{\mathcal M}) = \aleph _1$
and second that
![]() $\mathfrak b (\in ^*_{\mathcal N}) = \mathfrak b (\neq ^*_{\mathcal N}) = \kappa ^+$
. The first one is easy. Recall that (iterated) Cohen forcing does not add a slalom eventually capturing all the ground model reals, nor an eventually different function and both
$\mathfrak b (\in ^*_{\mathcal N}) = \mathfrak b (\neq ^*_{\mathcal N}) = \kappa ^+$
. The first one is easy. Recall that (iterated) Cohen forcing does not add a slalom eventually capturing all the ground model reals, nor an eventually different function and both
![]() ${\textrm {cov}}(\mathcal M)$
and
${\textrm {cov}}(\mathcal M)$
and
![]() $\mathfrak {d}$
(
$\mathfrak {d}$
(
![]() $= {\textrm {cov}} (\mathcal K)$
) are
$= {\textrm {cov}} (\mathcal K)$
) are
![]() $\kappa $
so Lemma 3.2 applies.
$\kappa $
so Lemma 3.2 applies.
The second argument is slightly more involved. We need to verify that there is a
![]() $(\kappa , \aleph _1)$
-Rothberger family for the null ideal as described in Lemma 3.5. Let G be V-generic for the product of
$(\kappa , \aleph _1)$
-Rothberger family for the null ideal as described in Lemma 3.5. Let G be V-generic for the product of
![]() $\kappa $
many Cohen reals and work in
$\kappa $
many Cohen reals and work in
![]() $V[G]$
. Let
$V[G]$
. Let
![]() $\{c_\alpha \; | \; \alpha < \kappa \}$
enumerate the Cohen reals. Each such real, say
$\{c_\alpha \; | \; \alpha < \kappa \}$
enumerate the Cohen reals. Each such real, say
![]() $c_\alpha $
, codes a null set
$c_\alpha $
, codes a null set
![]() $N_\alpha $
. It is this family
$N_\alpha $
. It is this family
![]() $\{N_\alpha \; | \; \alpha < \kappa \}$
that will witness the lemma. It remains to see that any
$\{N_\alpha \; | \; \alpha < \kappa \}$
that will witness the lemma. It remains to see that any
![]() $\aleph _1$
-sized subset is covering.
$\aleph _1$
-sized subset is covering.
By the ccc, for each
![]() $x:\omega \to \omega $
there is a countable
$x:\omega \to \omega $
there is a countable
![]() $X \subseteq \kappa $
so that in fact x is added by the forcing restricted to X. Let us denote, for
$X \subseteq \kappa $
so that in fact x is added by the forcing restricted to X. Let us denote, for
![]() $\dot {x}$
a name for a real
$\dot {x}$
a name for a real
![]() $X_{\dot {x}}$
the countable support as described above. Observe that if
$X_{\dot {x}}$
the countable support as described above. Observe that if
![]() $\alpha \notin X_{\dot x}$
then in fact
$\alpha \notin X_{\dot x}$
then in fact
![]() $\dot {x}$
is forced to be in
$\dot {x}$
is forced to be in
![]() $N_\alpha $
by mutual genericity of the Cohen reals. But now, given any
$N_\alpha $
by mutual genericity of the Cohen reals. But now, given any
![]() $\aleph _1$
-sized family
$\aleph _1$
-sized family
![]() $\mathcal Y \subseteq \{N_\alpha \; | \; \alpha < \kappa \}$
and any name for a real
$\mathcal Y \subseteq \{N_\alpha \; | \; \alpha < \kappa \}$
and any name for a real
![]() $\dot {x}$
, it must be the case that there is an
$\dot {x}$
, it must be the case that there is an
![]() $N_\alpha \in \mathcal Y$
so that
$N_\alpha \in \mathcal Y$
so that
![]() $\alpha \notin X_{\dot {x}}$
so
$\alpha \notin X_{\dot {x}}$
so
![]() $x \in N_\alpha $
as needed.
$x \in N_\alpha $
as needed.
4.2 The random model
The random model is the model obtained by forcing with the random forcing
![]() $\mathbb B_\kappa $
for the measure algebra
$\mathbb B_\kappa $
for the measure algebra
![]() $2^\kappa $
over a model of
$2^\kappa $
over a model of
![]() $\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.6.8, p. 393]. We will prove the following theorem.
$\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.6.8, p. 393]. We will prove the following theorem.
Theorem 4.3. In the random model the following hold.
-
(1) For all
 $R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
 $\mathfrak b (R_{\mathcal M})= \kappa ^+$
.
$\mathfrak b (R_{\mathcal M})= \kappa ^+$
. -
(2)
 $\mathfrak b (\in ^*_{\mathcal N}) = \mathfrak b(\leq ^*_{\mathcal N}) = \aleph _1$
.
$\mathfrak b (\in ^*_{\mathcal N}) = \mathfrak b(\leq ^*_{\mathcal N}) = \aleph _1$
. -
(3)
 $\mathfrak b (\neq ^*_{\mathcal N}) = \mathfrak b(\neq ^*_{\mathcal K}) = \kappa $
.
$\mathfrak b (\neq ^*_{\mathcal N}) = \mathfrak b(\neq ^*_{\mathcal K}) = \kappa $
. -
(4)
 $\mathfrak b (\in ^*_{\mathcal K}) = \mathfrak b(\leq ^*_{\mathcal K}) = \aleph _2$
.
$\mathfrak b (\in ^*_{\mathcal K}) = \mathfrak b(\leq ^*_{\mathcal K}) = \aleph _2$
.
Observe from this theorem the somewhat surprising constellation given by looking at the cardinals associated with
![]() $\in ^*$
and
$\in ^*$
and
![]() $\leq ^*$
. Namely we have that
$\leq ^*$
. Namely we have that
![]() $\mathfrak b(\in ^*_{\mathcal N}) = \aleph _1 < \mathfrak b(\in ^*_{\mathcal K}) = \aleph _2 < \mathfrak b (\in ^*_{\mathcal M}) = \kappa ^+$
, and similarly for
$\mathfrak b(\in ^*_{\mathcal N}) = \aleph _1 < \mathfrak b(\in ^*_{\mathcal K}) = \aleph _2 < \mathfrak b (\in ^*_{\mathcal M}) = \kappa ^+$
, and similarly for
![]() $\leq ^*$
. We do not know whether it is consistent that the three cardinals related to
$\leq ^*$
. We do not know whether it is consistent that the three cardinals related to
![]() $\neq ^*$
are simultaneously distinct.
$\neq ^*$
are simultaneously distinct.
Proof Let
![]() $G \subseteq \mathbb B_\kappa $
be generic over V and enumerate the
$G \subseteq \mathbb B_\kappa $
be generic over V and enumerate the
![]() $\kappa $
-many random reals as
$\kappa $
-many random reals as
![]() $\{r_\alpha \; | \; \alpha < \kappa \}$
. We argue for each point individually, starting with the cardinals for the meager ideal. This argument is almost verbatim the same as the argument in the case of the cardinals associated with the null ideal in the Cohen model. The difference is that each random real
$\{r_\alpha \; | \; \alpha < \kappa \}$
. We argue for each point individually, starting with the cardinals for the meager ideal. This argument is almost verbatim the same as the argument in the case of the cardinals associated with the null ideal in the Cohen model. The difference is that each random real
![]() $r_\alpha $
codes a meager set
$r_\alpha $
codes a meager set
![]() $M_\alpha $
.
$M_\alpha $
.
The second item follows from Lemma 3.2 noting that random forcing makes
![]() ${\textrm {cov}}(\mathcal N) = \kappa $
and is
${\textrm {cov}}(\mathcal N) = \kappa $
and is
![]() $\omega ^\omega $
-bounding.
$\omega ^\omega $
-bounding.
For the third, note first that
![]() $\mathfrak b(\neq ^*)$
(
$\mathfrak b(\neq ^*)$
(
![]() $= {\textrm {non}}(\mathcal M)$
) is
$= {\textrm {non}}(\mathcal M)$
) is
![]() $\kappa $
in the random model since every random real adds an eventually different real. It follows that
$\kappa $
in the random model since every random real adds an eventually different real. It follows that
![]() $\kappa = \mathfrak b(\neq ^*) \leq \mathfrak b(\neq ^*_{\mathcal N}) = \mathfrak b(\neq ^*_{\mathcal K})$
so we get the lower bound. Conversely, note that
$\kappa = \mathfrak b(\neq ^*) \leq \mathfrak b(\neq ^*_{\mathcal N}) = \mathfrak b(\neq ^*_{\mathcal K})$
so we get the lower bound. Conversely, note that
![]() ${\textrm {non}}(\mathcal N) = {\textrm {non}}(\mathcal K) = \mathfrak b = \aleph _1$
in the random model so by Lemma 1.4 we get
${\textrm {non}}(\mathcal N) = {\textrm {non}}(\mathcal K) = \mathfrak b = \aleph _1$
in the random model so by Lemma 1.4 we get
![]() $\mathfrak b(\neq ^*_{\mathcal N}) \leq \mathfrak b(\neq ^*)^{{\textrm {non}}(\mathcal N)} = \kappa ^{\aleph _1} = \kappa $
and the same for
$\mathfrak b(\neq ^*_{\mathcal N}) \leq \mathfrak b(\neq ^*)^{{\textrm {non}}(\mathcal N)} = \kappa ^{\aleph _1} = \kappa $
and the same for
![]() $\mathfrak b(\neq ^*_{\mathcal K})$
.
$\mathfrak b(\neq ^*_{\mathcal K})$
.
For the fourth, the lower bound comes from the fact that
![]() $\mathfrak {d} = \aleph _1$
so by Lemma 3.3 we get
$\mathfrak {d} = \aleph _1$
so by Lemma 3.3 we get
![]() $\aleph _2 \leq \mathfrak b (\in ^*_{\mathcal K}) \leq \mathfrak b(\leq ^*_{\mathcal K})$
. The upper bound is proved in exactly the same manner as Lemma 4.1.
$\aleph _2 \leq \mathfrak b (\in ^*_{\mathcal K}) \leq \mathfrak b(\leq ^*_{\mathcal K})$
. The upper bound is proved in exactly the same manner as Lemma 4.1.
4.3 The Sacks model
The Sacks model refers to either the countable support product or iteration of
![]() $\kappa $
many copies of Sacks forcing,
$\kappa $
many copies of Sacks forcing,
![]() $\mathbb S$
, over a model of
$\mathbb S$
, over a model of
![]() $\mathsf {GCH}$
, where in the later case we must insist
$\mathsf {GCH}$
, where in the later case we must insist
![]() $\kappa = \aleph _2$
, see [Reference Bartoszyński and Judah1, Model 7.6.2, p. 388]. It turns out that the computation of the cardinals is unchanged regardless of whether we take the product or the iteration.
$\kappa = \aleph _2$
, see [Reference Bartoszyński and Judah1, Model 7.6.2, p. 388]. It turns out that the computation of the cardinals is unchanged regardless of whether we take the product or the iteration.
Theorem 4.4. For all R and
![]() $\mathcal I$
, in the side by side or iterated Sacks model
$\mathcal I$
, in the side by side or iterated Sacks model
![]() $\mathfrak b (R_{\mathcal I}) = \aleph _2$
.
$\mathfrak b (R_{\mathcal I}) = \aleph _2$
.
Proof This follows in a straightforward way from the Sacks property by combining Lemma 3.3 and Lemmas 4.1 and 1.4. In particular, the Sacks property ensures that all covering numbers are small so
![]() $\aleph _2$
is a lower bound and the hypotheses of Lemma 4.1 (for the side by side)/the cardinals in Lemma 1.4 (for the iteration) are also met thanks to the Sacks property so
$\aleph _2$
is a lower bound and the hypotheses of Lemma 4.1 (for the side by side)/the cardinals in Lemma 1.4 (for the iteration) are also met thanks to the Sacks property so
![]() $\aleph _2$
is the upper bound as well.
$\aleph _2$
is the upper bound as well.
This is somewhat surprising since this means that some higher dimensional cardinals are bigger in the Sacks model than in the Cohen and random models.
4.4 The Hechler model
By the Hechler model we mean the finite support iteration of Hechler forcing,
![]() $\mathbb D$
, over a model
$\mathbb D$
, over a model
![]() $\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.6.9, p. 394].
$\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.6.9, p. 394].
Theorem 4.5. In the Hechler model the following hold.
-
(1) For R equal to
 $\leq ^*$
or
$\leq ^*$
or
 $\neq ^*$
, we have that
$\neq ^*$
, we have that
 $\mathfrak b(R_{\mathcal I}) = \kappa ^+$
for all
$\mathfrak b(R_{\mathcal I}) = \kappa ^+$
for all
 $\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
.
$\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
. -
(2)
 $\mathfrak b (\in ^*_{\mathcal K}) = \mathfrak b (\in ^*_{\mathcal M}) = \aleph _1$
.
$\mathfrak b (\in ^*_{\mathcal K}) = \mathfrak b (\in ^*_{\mathcal M}) = \aleph _1$
. -
(3)
 $\mathfrak b (\in ^*_{\mathcal N}) = \kappa ^+$
.
$\mathfrak b (\in ^*_{\mathcal N}) = \kappa ^+$
.
Proof Let G be generic over V for the iteration
![]() $\mathbb D_\kappa $
. Denote the
$\mathbb D_\kappa $
. Denote the
![]() $\alpha {\textrm {th}}$
stage of the iteration by
$\alpha {\textrm {th}}$
stage of the iteration by
![]() $\mathbb D_\alpha $
and let
$\mathbb D_\alpha $
and let
![]() $\{d_\alpha \; | \; \alpha < \kappa \}$
be the
$\{d_\alpha \; | \; \alpha < \kappa \}$
be the
![]() $\kappa $
many Hechler reals added by G. Since each Hechler real is dominating, and also adds a Cohen real, it is well known that in the Hechler model
$\kappa $
many Hechler reals added by G. Since each Hechler real is dominating, and also adds a Cohen real, it is well known that in the Hechler model
![]() $\mathfrak b = {\textrm {cov}}(\mathcal M) = \kappa $
. As a result, Lemma 3.1 ensures the first part. For the second part, it suffices to observe that in the Hechler model
$\mathfrak b = {\textrm {cov}}(\mathcal M) = \kappa $
. As a result, Lemma 3.1 ensures the first part. For the second part, it suffices to observe that in the Hechler model
![]() ${\textrm {cov}} (\mathcal M) = \kappa $
, but no slalom is added eventually capturing all ground model reals so Lemma 3.2 applies.
${\textrm {cov}} (\mathcal M) = \kappa $
, but no slalom is added eventually capturing all ground model reals so Lemma 3.2 applies.
The last item requires more argument and involves verifying the existence of a
![]() $(\kappa , \aleph _1)$
-Rothberger family as in Lemma 3.5. Each Hechler real adds a Cohen real, and the null sets coded by these Cohen reals will be our family. Towards proving this fact, fix a partition
$(\kappa , \aleph _1)$
-Rothberger family as in Lemma 3.5. Each Hechler real adds a Cohen real, and the null sets coded by these Cohen reals will be our family. Towards proving this fact, fix a partition
![]() $\langle I_k\; | \; k \in \omega \rangle $
of
$\langle I_k\; | \; k \in \omega \rangle $
of
![]() $\omega $
into finite intervals with
$\omega $
into finite intervals with
![]() $|I_k| = k+1$
. We start with some facts about finite support iterations of
$|I_k| = k+1$
. We start with some facts about finite support iterations of
![]() $\sigma $
-centered forcing notions
$\sigma $
-centered forcing notions
![]() $\langle \mathbb P_\alpha , \dot {\mathbb Q}_\alpha \; | \; \alpha < \kappa \rangle $
. The first is well-known.
$\langle \mathbb P_\alpha , \dot {\mathbb Q}_\alpha \; | \; \alpha < \kappa \rangle $
. The first is well-known.
Fact 4.6. Let
![]() $\langle \mathbb P_\alpha , \dot {\mathbb Q}_\alpha \; | \; \alpha < \kappa \rangle $
be a finite support iteration of
$\langle \mathbb P_\alpha , \dot {\mathbb Q}_\alpha \; | \; \alpha < \kappa \rangle $
be a finite support iteration of
![]() $\sigma $
-centered forcing notions. Let
$\sigma $
-centered forcing notions. Let
![]() $\alpha \leq \beta \leq \kappa $
and let
$\alpha \leq \beta \leq \kappa $
and let
![]() $\dot {x}$
be a
$\dot {x}$
be a
![]() $\mathbb P_\beta $
-name for an element of
$\mathbb P_\beta $
-name for an element of
![]() $2^\omega $
. Then there are
$2^\omega $
. Then there are
![]() $\mathbb P_\alpha $
-names
$\mathbb P_\alpha $
-names
![]() $\{\dot {x}_n \in 2^\omega \; | \; n \in \omega \}$
so that for all
$\{\dot {x}_n \in 2^\omega \; | \; n \in \omega \}$
so that for all
![]() $\mathbb P_\alpha $
-names
$\mathbb P_\alpha $
-names
![]() $\dot {y}$
forced to be in
$\dot {y}$
forced to be in
![]() $2^\omega $
if
$2^\omega $
if
![]() $\Vdash _\alpha \forall n \exists ^\infty k ( \dot {x}_n \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
then
$\Vdash _\alpha \forall n \exists ^\infty k ( \dot {x}_n \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
then
![]() $\Vdash _\beta \exists ^\infty k (\dot {x} \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
.
$\Vdash _\beta \exists ^\infty k (\dot {x} \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
.
Proof of 4.6 By working in
![]() $V^{\mathbb P_\alpha }$
we may assume without loss of generality that
$V^{\mathbb P_\alpha }$
we may assume without loss of generality that
![]() $\alpha = 0$
. The proof is by induction on
$\alpha = 0$
. The proof is by induction on
![]() $\beta $
. The case where
$\beta $
. The case where
![]() $\beta = 0$
is trivial hence we may suppose that
$\beta = 0$
is trivial hence we may suppose that
![]() $\beta> 0$
. First assume that
$\beta> 0$
. First assume that
![]() $\beta = \gamma + 1$
for some
$\beta = \gamma + 1$
for some
![]() $\gamma $
and work in
$\gamma $
and work in
![]() $V^{\mathbb P_\gamma }$
. Let
$V^{\mathbb P_\gamma }$
. Let
![]() $\mathbb Q_\gamma = \bigcup _{n < \omega } \mathbb Q_n$
be a partition of
$\mathbb Q_\gamma = \bigcup _{n < \omega } \mathbb Q_n$
be a partition of
![]() $\mathbb Q_\gamma $
into centered pieces. Fix
$\mathbb Q_\gamma $
into centered pieces. Fix
![]() $n, k \in \omega $
and define
$n, k \in \omega $
and define
![]() $x_n \upharpoonright I_k$
to be any value so that no
$x_n \upharpoonright I_k$
to be any value so that no
![]() $p \in \mathbb Q_n$
forces
$p \in \mathbb Q_n$
forces
![]() $\dot {x} \upharpoonright I_k \neq \check {x}_n \upharpoonright I_k$
. To see that such a value exists note that since
$\dot {x} \upharpoonright I_k \neq \check {x}_n \upharpoonright I_k$
. To see that such a value exists note that since
![]() $I_k$
is finite and
$I_k$
is finite and
![]() $\mathbb Q_n$
is centered, if for each
$\mathbb Q_n$
is centered, if for each
![]() $s \in 2^{I_k}$
there was a condition in
$s \in 2^{I_k}$
there was a condition in
![]() $\mathbb Q_n$
forcing
$\mathbb Q_n$
forcing
![]() $\dot x \upharpoonright I_k \neq s$
, then a common extension of these conditions would force a contradictory statement. If
$\dot x \upharpoonright I_k \neq s$
, then a common extension of these conditions would force a contradictory statement. If
![]() $y \in 2^\omega \cap V^{\mathbb P_\gamma }$
is equal to
$y \in 2^\omega \cap V^{\mathbb P_\gamma }$
is equal to
![]() $x_n \upharpoonright I_k$
for infinitely many k and all n then
$x_n \upharpoonright I_k$
for infinitely many k and all n then
![]() $\Vdash _{\gamma + 1} \exists ^\infty k \, \check {y} \upharpoonright I_k =\dot {x} \upharpoonright I_k$
. This is because otherwise there would be a natural numbers
$\Vdash _{\gamma + 1} \exists ^\infty k \, \check {y} \upharpoonright I_k =\dot {x} \upharpoonright I_k$
. This is because otherwise there would be a natural numbers
![]() $n, l \in \omega $
and a condition
$n, l \in \omega $
and a condition
![]() $p \in \mathbb Q_n$
so that
$p \in \mathbb Q_n$
so that
![]() $p \Vdash \forall k> l \, \check {y} \upharpoonright I_k \neq \dot {x} \upharpoonright I_k$
but by the way we constructed the
$p \Vdash \forall k> l \, \check {y} \upharpoonright I_k \neq \dot {x} \upharpoonright I_k$
but by the way we constructed the
![]() $x_n$
’s, we can find a
$x_n$
’s, we can find a
![]() $q \leq p$
and an
$q \leq p$
and an
![]() $j> l$
so that
$j> l$
so that
![]() $y \upharpoonright I_j = x_n \upharpoonright I_j$
and
$y \upharpoonright I_j = x_n \upharpoonright I_j$
and
![]() $q \Vdash \dot {x} \upharpoonright I_j = \check {x}_n \upharpoonright I_j$
. Now, let
$q \Vdash \dot {x} \upharpoonright I_j = \check {x}_n \upharpoonright I_j$
. Now, let
![]() $\dot {x}_n$
name
$\dot {x}_n$
name
![]() $x_n$
in V and apply the inductive hypothesis to each
$x_n$
in V and apply the inductive hypothesis to each
![]() $\dot {x}_n$
to get elements of
$\dot {x}_n$
to get elements of
![]() $2^\omega $
, say
$2^\omega $
, say
![]() $\{x_{n, m} \; | \; n, m \in \omega \}$
so that for each
$\{x_{n, m} \; | \; n, m \in \omega \}$
so that for each
![]() $n <\omega $
and y we have that if
$n <\omega $
and y we have that if
![]() $\forall m \exists ^\infty k \, (y \upharpoonright I_k =x_{n, m} \upharpoonright I_k)$
then
$\forall m \exists ^\infty k \, (y \upharpoonright I_k =x_{n, m} \upharpoonright I_k)$
then
![]() $\Vdash _\gamma \exists ^\infty k (\check {y} \upharpoonright I_k = \dot {x}_n \upharpoonright I_k)$
. Then using the countable set
$\Vdash _\gamma \exists ^\infty k (\check {y} \upharpoonright I_k = \dot {x}_n \upharpoonright I_k)$
. Then using the countable set
![]() $\{x_{n, m} \; | \; n, m \in \omega \}$
for the
$\{x_{n, m} \; | \; n, m \in \omega \}$
for the
![]() $\dot{x}_n$
’s witness the fact in this case.
$\dot{x}_n$
’s witness the fact in this case.
Now suppose that
![]() $\beta $
is a limit ordinal. Since
$\beta $
is a limit ordinal. Since
![]() $\dot {x}$
names a real, we can assume without loss of generality that
$\dot {x}$
names a real, we can assume without loss of generality that
![]() $\beta $
has countable cofinality. Let
$\beta $
has countable cofinality. Let
![]() $\langle \gamma _n \; | \; n\in \omega \rangle $
be a strictly increasing sequence of ordinals with limit
$\langle \gamma _n \; | \; n\in \omega \rangle $
be a strictly increasing sequence of ordinals with limit
![]() $\beta $
. For each
$\beta $
. For each
![]() $n < \omega $
find a decreasing set of conditions in
$n < \omega $
find a decreasing set of conditions in
![]() $V^{\mathbb P_{\gamma _n}}$
deciding all of
$V^{\mathbb P_{\gamma _n}}$
deciding all of
![]() $\dot {x}$
and let
$\dot {x}$
and let
![]() $x_n \in V^{\mathbb P_{\gamma _n}}$
be the real interpreting
$x_n \in V^{\mathbb P_{\gamma _n}}$
be the real interpreting
![]() $\dot {x}$
based on these decisions. Let
$\dot {x}$
based on these decisions. Let
![]() $\dot {x}_n$
be a name for
$\dot {x}_n$
be a name for
![]() $x_n$
in V and, applying the inductive hypothesis to each
$x_n$
in V and, applying the inductive hypothesis to each
![]() $x_n$
let
$x_n$
let
![]() $\{x_{n, m} \; | \; m \in \omega \}$
be a set of reals so that for each
$\{x_{n, m} \; | \; m \in \omega \}$
be a set of reals so that for each
![]() $n <\omega $
and y we have that if
$n <\omega $
and y we have that if
![]() $\forall m \exists ^\infty k \, (y \upharpoonright I_k =x_{n, m} \upharpoonright I_k)$
then
$\forall m \exists ^\infty k \, (y \upharpoonright I_k =x_{n, m} \upharpoonright I_k)$
then
![]() $\Vdash _{\gamma _n} \exists ^\infty k \, (\check {y} \upharpoonright I_k = \dot {x}_n \upharpoonright I_k)$
. We claim that these
$\Vdash _{\gamma _n} \exists ^\infty k \, (\check {y} \upharpoonright I_k = \dot {x}_n \upharpoonright I_k)$
. We claim that these
![]() $\{x_{n, m} \; | \;n, m \in \omega \}$
work for
$\{x_{n, m} \; | \;n, m \in \omega \}$
work for
![]() $\dot {x}$
. To see this, suppose that for all n and m there are infinitely many k so that
$\dot {x}$
. To see this, suppose that for all n and m there are infinitely many k so that
![]() $x_{n, m} \upharpoonright I_k = y \upharpoonright I_k$
but there is an
$x_{n, m} \upharpoonright I_k = y \upharpoonright I_k$
but there is an
![]() $l \in \omega $
and a
$l \in \omega $
and a
![]() $p \in \mathbb P_\beta $
so that
$p \in \mathbb P_\beta $
so that
![]() $p \Vdash _\beta \forall k> l \;( \dot {x} \upharpoonright I_k \neq \check {y} \upharpoonright I_k)$
. By the finiteness of the support, p is actually a
$p \Vdash _\beta \forall k> l \;( \dot {x} \upharpoonright I_k \neq \check {y} \upharpoonright I_k)$
. By the finiteness of the support, p is actually a
![]() $\mathbb P_{\gamma _n}$
condition for some
$\mathbb P_{\gamma _n}$
condition for some
![]() $n < \omega $
and, by assumption
$n < \omega $
and, by assumption
![]() $p \Vdash _{\gamma _n} \exists ^\infty k \, (\dot {x}_n \upharpoonright I_k = \check {y} \upharpoonright I_k)$
. However, by the construction of the
$p \Vdash _{\gamma _n} \exists ^\infty k \, (\dot {x}_n \upharpoonright I_k = \check {y} \upharpoonright I_k)$
. However, by the construction of the
![]() $x_n$
’s we can find an
$x_n$
’s we can find an
![]() $r \leq _{\beta } p$
and a
$r \leq _{\beta } p$
and a
![]() $k> l$
so that
$k> l$
so that
![]() $r \Vdash _{\beta } \dot {x} \upharpoonright I_k = \dot {x}_n \upharpoonright I_k = \check {y} \upharpoonright I_k$
which is a contradiction.
$r \Vdash _{\beta } \dot {x} \upharpoonright I_k = \dot {x}_n \upharpoonright I_k = \check {y} \upharpoonright I_k$
which is a contradiction.
Now for some
![]() $\beta \leq \kappa $
let
$\beta \leq \kappa $
let
![]() $\dot {x}$
be a
$\dot {x}$
be a
![]() $\mathbb D_\beta $
-name for an element of
$\mathbb D_\beta $
-name for an element of
![]() $2^\omega $
and define inductively on
$2^\omega $
and define inductively on
![]() $\beta \leq \kappa $
the hereditary support of
$\beta \leq \kappa $
the hereditary support of
![]() $\dot {x}$
, denoted
$\dot {x}$
, denoted
![]() ${\textrm {supp}}(\dot {x})$
, as follows. If
${\textrm {supp}}(\dot {x})$
, as follows. If
![]() $\beta = 0$
then
$\beta = 0$
then
![]() ${\textrm {supp}}(\dot {x}) = \emptyset $
. If
${\textrm {supp}}(\dot {x}) = \emptyset $
. If
![]() $\beta = \gamma + 1$
, let
$\beta = \gamma + 1$
, let
![]() $(\dot {x}_n\; | \; n \in \omega )$
be the
$(\dot {x}_n\; | \; n \in \omega )$
be the
![]() $\mathbb D_\gamma $
-names constructed from
$\mathbb D_\gamma $
-names constructed from
![]() $\dot {x}$
as in Fact 4.6 and let
$\dot {x}$
as in Fact 4.6 and let
![]() $\{p_{m, k}\; | \; k \in \omega \}$
be a maximal antichain deciding
$\{p_{m, k}\; | \; k \in \omega \}$
be a maximal antichain deciding
![]() $\dot {x}(\check {m})$
. Set
$\dot {x}(\check {m})$
. Set
If
![]() $\beta $
is a limit of countable cofinality, let
$\beta $
is a limit of countable cofinality, let
![]() $(\gamma _n \; | \; n< \omega )$
be a strictly increasing sequence of ordinals whose limit is
$(\gamma _n \; | \; n< \omega )$
be a strictly increasing sequence of ordinals whose limit is
![]() $\beta $
, for each
$\beta $
, for each
![]() $n < \omega $
let
$n < \omega $
let
![]() $\{\dot {x}_{n, m} \; | \; m \in \omega \}$
be the
$\{\dot {x}_{n, m} \; | \; m \in \omega \}$
be the
![]() $\mathbb D_{\gamma _n}$
-names constructed from
$\mathbb D_{\gamma _n}$
-names constructed from
![]() $\dot {x}$
as in Fact 4.6 and let
$\dot {x}$
as in Fact 4.6 and let
where
![]() $p_{m, k}$
are as before. Finally for
$p_{m, k}$
are as before. Finally for
![]() $\beta $
a limit ordinal of uncountable cofinality observe that, by the finite support, there is a
$\beta $
a limit ordinal of uncountable cofinality observe that, by the finite support, there is a
![]() $\gamma < \beta $
so that
$\gamma < \beta $
so that
![]() $\dot {x}$
is in fact equivalent to a
$\dot {x}$
is in fact equivalent to a
![]() $\mathbb D_\gamma $
-name. Let
$\mathbb D_\gamma $
-name. Let
![]() ${\textrm {supp}}(\dot {x})$
be the support of this
${\textrm {supp}}(\dot {x})$
be the support of this
![]() $\mathbb D_\gamma $
-name. Note that in all cases
$\mathbb D_\gamma $
-name. Note that in all cases
![]() ${\textrm {supp}}(\dot {x})$
is a countable set of ordinals. We need another fact.
${\textrm {supp}}(\dot {x})$
is a countable set of ordinals. We need another fact.
Fact 4.7. Let
![]() $\alpha < \alpha ' \leq \beta \leq \kappa $
and let
$\alpha < \alpha ' \leq \beta \leq \kappa $
and let
![]() $\dot {x}$
be a
$\dot {x}$
be a
![]() $\mathbb D_\beta $
-name for an element of
$\mathbb D_\beta $
-name for an element of
![]() $2^\omega $
. Assume
$2^\omega $
. Assume
![]() ${\textrm {supp}}(\dot {x}) \cap [\alpha , \alpha ') = \emptyset $
. Then there are
${\textrm {supp}}(\dot {x}) \cap [\alpha , \alpha ') = \emptyset $
. Then there are
![]() $\mathbb D_\alpha $
-names for elements of
$\mathbb D_\alpha $
-names for elements of
![]() $2^\omega $
,
$2^\omega $
,
![]() $\{\dot {x}_n\; | \; n \in \omega \}$
, so that for all
$\{\dot {x}_n\; | \; n \in \omega \}$
, so that for all
![]() $\mathbb D_{\alpha '}$
-names
$\mathbb D_{\alpha '}$
-names
![]() $\dot {y}$
for elements of
$\dot {y}$
for elements of
![]() $2^\omega $
, if
$2^\omega $
, if
![]() $\Vdash _{\alpha '} \forall n \exists ^\infty k \, (\dot {x}_n \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
, then
$\Vdash _{\alpha '} \forall n \exists ^\infty k \, (\dot {x}_n \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
, then
![]() $\Vdash _\beta \exists ^\infty k \, (\dot {x} \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
.
$\Vdash _\beta \exists ^\infty k \, (\dot {x} \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
.
Proof of 4.7 The proof is by induction on
![]() $\beta $
. If
$\beta $
. If
![]() $\beta = \alpha '$
or
$\beta = \alpha '$
or
![]() $\beta = 0$
then the fact is trivially true so assume
$\beta = 0$
then the fact is trivially true so assume
![]() $0 \leq \alpha < \alpha ' < \beta $
. There are two cases corresponding to whether
$0 \leq \alpha < \alpha ' < \beta $
. There are two cases corresponding to whether
![]() $\beta $
is a successor or a limit.
$\beta $
is a successor or a limit.
First suppose that
![]() $\beta = \gamma + 1$
for some
$\beta = \gamma + 1$
for some
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $\{\dot {x}_n\; | \; n \in \omega \}$
be
$\{\dot {x}_n\; | \; n \in \omega \}$
be
![]() $\mathbb D_\gamma $
-names as constructed in the proof of Fact 4.6. By the definition of the support plus the assumption that
$\mathbb D_\gamma $
-names as constructed in the proof of Fact 4.6. By the definition of the support plus the assumption that
![]() ${\textrm {supp}}(\dot {x}) \cap [\alpha , \alpha ') = \emptyset $
we get that
${\textrm {supp}}(\dot {x}) \cap [\alpha , \alpha ') = \emptyset $
we get that
![]() ${\textrm {supp}}(\dot {x}_n) \cap [\alpha , \alpha ') = \emptyset $
for all
${\textrm {supp}}(\dot {x}_n) \cap [\alpha , \alpha ') = \emptyset $
for all
![]() $n < \omega $
. Applying the inductive hypothesis we get for each
$n < \omega $
. Applying the inductive hypothesis we get for each
![]() $n < \omega $
a countable set of
$n < \omega $
a countable set of
![]() $\mathbb D_\alpha $
-names
$\mathbb D_\alpha $
-names
![]() $\{\dot {x}_{n, m} \; | \; m \in \omega \}$
so that for all
$\{\dot {x}_{n, m} \; | \; m \in \omega \}$
so that for all
![]() $\mathbb D_{\alpha '}$
-names
$\mathbb D_{\alpha '}$
-names
![]() $\dot {y}$
for elements of
$\dot {y}$
for elements of
![]() $2^\omega $
, if
$2^\omega $
, if
![]() $\Vdash _{\alpha '} \forall m \exists ^\infty k \, (\dot {x}_{n, m} \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
, then
$\Vdash _{\alpha '} \forall m \exists ^\infty k \, (\dot {x}_{n, m} \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
, then
![]() $\Vdash _\beta \exists ^\infty k \,( \dot {x}_n \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
. Using these the same way as in the proof of Fact 4.6 completes the proof of this case.
$\Vdash _\beta \exists ^\infty k \,( \dot {x}_n \upharpoonright I_k = \dot {y} \upharpoonright I_k)$
. Using these the same way as in the proof of Fact 4.6 completes the proof of this case.
Suppose now that
![]() $\beta $
is a limit ordinal. Since
$\beta $
is a limit ordinal. Since
![]() $\dot {x}$
is a
$\dot {x}$
is a
![]() $\mathbb D_\beta $
-name for a real, we can reduce to the case where
$\mathbb D_\beta $
-name for a real, we can reduce to the case where
![]() $\beta $
has countable cofinality. Let
$\beta $
has countable cofinality. Let
![]() $\langle \gamma _n \; | \; n < \omega \rangle $
be a strictly increasing sequence of ordinals whose limit is
$\langle \gamma _n \; | \; n < \omega \rangle $
be a strictly increasing sequence of ordinals whose limit is
![]() $\beta $
. For each
$\beta $
. For each
![]() $n < \omega $
let
$n < \omega $
let
![]() $\{\dot {x}_{n, m} \; | \; m \in \omega \}$
be the
$\{\dot {x}_{n, m} \; | \; m \in \omega \}$
be the
![]() $\mathbb D_{\gamma _n}$
-names constructed from
$\mathbb D_{\gamma _n}$
-names constructed from
![]() $\dot {x}$
as in Fact 4.6. Using these countably many names the rest of the proof of this case is the same as in the successor case.
$\dot {x}$
as in Fact 4.6. Using these countably many names the rest of the proof of this case is the same as in the successor case.
Note that if
![]() $y \in 2^\omega $
then the set
$y \in 2^\omega $
then the set
![]() $N_y = \{x \in 2^\omega \; | \; \exists ^\infty k \, (x\upharpoonright I_k = y \upharpoonright I_k) \}$
is a null set. Let
$N_y = \{x \in 2^\omega \; | \; \exists ^\infty k \, (x\upharpoonright I_k = y \upharpoonright I_k) \}$
is a null set. Let
![]() $c_\alpha $
be the Cohen real added by the
$c_\alpha $
be the Cohen real added by the
![]() $\alpha ^{\textrm {th}}$
-Hechler real.
$\alpha ^{\textrm {th}}$
-Hechler real.
Claim 4.8. If
![]() $\dot {x}$
is a
$\dot {x}$
is a
![]() $\mathbb P_\kappa $
-name for an element of
$\mathbb P_\kappa $
-name for an element of
![]() $2^\omega $
and
$2^\omega $
and
![]() $\alpha \notin {\textrm {supp}}(\dot {x})$
then
$\alpha \notin {\textrm {supp}}(\dot {x})$
then
![]() $\Vdash _\kappa \dot {x} \in N_{\dot {c}_\alpha }$
.
$\Vdash _\kappa \dot {x} \in N_{\dot {c}_\alpha }$
.
Proof of Claim Fix
![]() $\alpha < \kappa $
. It’s well known that for all
$\alpha < \kappa $
. It’s well known that for all
![]() $\mathbb D_\alpha $
-names
$\mathbb D_\alpha $
-names
![]() $\dot {z}$
for elements of
$\dot {z}$
for elements of
![]() $2^\omega $
we have
$2^\omega $
we have
![]() $\Vdash _{\alpha + 1} \exists ^\infty k \, (\dot {z} \upharpoonright I_k = \dot {c}_\alpha \upharpoonright I_k)$
. Now the claim follows by applying Fact 4.7 to
$\Vdash _{\alpha + 1} \exists ^\infty k \, (\dot {z} \upharpoonright I_k = \dot {c}_\alpha \upharpoonright I_k)$
. Now the claim follows by applying Fact 4.7 to
![]() $\alpha ' = \alpha + 1$
and
$\alpha ' = \alpha + 1$
and
![]() $\beta = \kappa $
.
$\beta = \kappa $
.
The proof is now essentially the same as that for Cohen forcing. Since
![]() ${\textrm {supp}}(\dot {x})$
is countable any
${\textrm {supp}}(\dot {x})$
is countable any
![]() $\aleph _1$
-sized subfamily of
$\aleph _1$
-sized subfamily of
![]() $\{N_{c_\alpha } \; | \; \alpha < \kappa \}$
must be covering.
$\{N_{c_\alpha } \; | \; \alpha < \kappa \}$
must be covering.
Let us note for later that the computation that
![]() $\mathfrak b(\in ^*_{\mathcal N}) = \kappa ^+$
relied solely on the facts that Hechler forcing is
$\mathfrak b(\in ^*_{\mathcal N}) = \kappa ^+$
relied solely on the facts that Hechler forcing is
![]() $\sigma $
-centered and adds Cohen reals.
$\sigma $
-centered and adds Cohen reals.
4.5 The dual random model
For any uncountable
![]() $\lambda \leq \kappa $
, the
$\lambda \leq \kappa $
, the
![]() $\lambda $
-dual random model is formed by first forcing
$\lambda $
-dual random model is formed by first forcing
![]() ${\textrm {add}}(\mathcal N) = \mathfrak {c} = \kappa $
by a ccc forcing and then adding
${\textrm {add}}(\mathcal N) = \mathfrak {c} = \kappa $
by a ccc forcing and then adding
![]() $\lambda $
-many random reals. The result, regardless of which
$\lambda $
-many random reals. The result, regardless of which
![]() $\lambda $
is chosen, the
$\lambda $
is chosen, the
![]() $\lambda $
-dual random model is a model where the values of the Cichoń diagram are determined by
$\lambda $
-dual random model is a model where the values of the Cichoń diagram are determined by
![]() ${\textrm {non}}(\mathcal N) = \aleph _1$
and
${\textrm {non}}(\mathcal N) = \aleph _1$
and
![]() ${\textrm {cov}}(\mathcal N) = \mathfrak b = \kappa $
.
${\textrm {cov}}(\mathcal N) = \mathfrak b = \kappa $
.
Theorem 4.9. In the
![]() $\lambda $
-dual random model, the following equalities hold.
$\lambda $
-dual random model, the following equalities hold.
-
(1)
 $\mathfrak b(\in ^*_{\mathcal N}) = \mathfrak b(\in ^*_{\mathcal K}) = \aleph _1$
.
$\mathfrak b(\in ^*_{\mathcal N}) = \mathfrak b(\in ^*_{\mathcal K}) = \aleph _1$
. -
(2)
 $\mathfrak b(\leq ^*_{\mathcal N}) = \mathfrak b(\neq ^*_{\mathcal N}) = \kappa $
.
$\mathfrak b(\leq ^*_{\mathcal N}) = \mathfrak b(\neq ^*_{\mathcal N}) = \kappa $
. -
(3)
 $\mathfrak b(\leq ^*_{\mathcal K}) = \mathfrak b(\neq ^*_{\mathcal K}) = \mathfrak b(\leq ^*_{\mathcal M}) = \mathfrak b(\neq ^*_{\mathcal M}) = \kappa ^+$
.
$\mathfrak b(\leq ^*_{\mathcal K}) = \mathfrak b(\neq ^*_{\mathcal K}) = \mathfrak b(\leq ^*_{\mathcal M}) = \mathfrak b(\neq ^*_{\mathcal M}) = \kappa ^+$
. -
(4)
 $\mathfrak b(\in ^*_{\mathcal M}) = \lambda ^+$
.
$\mathfrak b(\in ^*_{\mathcal M}) = \lambda ^+$
.
Let us note one interesting feature of this model. The value
![]() $\mathfrak b(\in ^*_{\mathcal M})$
depends on which
$\mathfrak b(\in ^*_{\mathcal M})$
depends on which
![]() $\lambda $
we chose, even though the cardinals in the Cichoń diagram are the same regardless of
$\lambda $
we chose, even though the cardinals in the Cichoń diagram are the same regardless of
![]() $\lambda $
. It follows that the
$\lambda $
. It follows that the
![]() $\mathfrak b(R_{\mathcal I})$
numbers are not uniquely determined by the values of the cardinal characteristics on
$\mathfrak b(R_{\mathcal I})$
numbers are not uniquely determined by the values of the cardinal characteristics on
![]() $\omega $
alongside cardinal arithmetic.
$\omega $
alongside cardinal arithmetic.
Proof For item 1 we can apply Lemma 3.2 since
![]() $\mathfrak b(\in ^*) = \aleph _1$
but the covering numbers for both
$\mathfrak b(\in ^*) = \aleph _1$
but the covering numbers for both
![]() $\mathcal K$
(
$\mathcal K$
(
![]() $=\mathfrak {d}$
) and
$=\mathfrak {d}$
) and
![]() $\mathcal N$
are of size continuum.
$\mathcal N$
are of size continuum.
For item 2 note we apply both inequalities in Lemma 1.4. On the one hand
![]() $\kappa $
is a lower bound since
$\kappa $
is a lower bound since
![]() $\mathfrak b= \mathfrak b(\neq ^*) = \kappa $
. On the other hand,
$\mathfrak b= \mathfrak b(\neq ^*) = \kappa $
. On the other hand,
![]() $\kappa $
is also an upper bound since
$\kappa $
is also an upper bound since
![]() $\mathfrak b^{{\textrm {non}}(\mathcal N)} = \kappa ^{\aleph _1} = \kappa $
.
$\mathfrak b^{{\textrm {non}}(\mathcal N)} = \kappa ^{\aleph _1} = \kappa $
.
Item 3 follows from Lemma 3.1 since
![]() $\mathfrak b = {\textrm {non}}(\mathcal M) = \kappa = 2^{\aleph _0}$
.
$\mathfrak b = {\textrm {non}}(\mathcal M) = \kappa = 2^{\aleph _0}$
.
Finally we tackle
![]() $\mathfrak b(\in ^*_{\mathcal M})$
. By the same argument used in Theorem 4.3,
$\mathfrak b(\in ^*_{\mathcal M})$
. By the same argument used in Theorem 4.3,
![]() $\mathfrak b(\in ^*_{\mathcal M})> \lambda $
as the
$\mathfrak b(\in ^*_{\mathcal M})> \lambda $
as the
![]() $\lambda $
random reals code
$\lambda $
random reals code
![]() $\lambda $
many meager sets forming a
$\lambda $
many meager sets forming a
![]() $(\lambda , \aleph _1)$
-Rothberger family. Also, for
$(\lambda , \aleph _1)$
-Rothberger family. Also, for
![]() $\lambda = \kappa $
,
$\lambda = \kappa $
,
![]() $\mathfrak b (\in ^*_{\mathcal M}) \leq 2^{\mathfrak {c}} = \mathfrak {c}^+ = \kappa ^+ = \lambda ^+$
.
$\mathfrak b (\in ^*_{\mathcal M}) \leq 2^{\mathfrak {c}} = \mathfrak {c}^+ = \kappa ^+ = \lambda ^+$
.
So assume
![]() $\lambda < \kappa $
. We will show that
$\lambda < \kappa $
. We will show that
![]() $\mathfrak {b} (\in ^*_{\mathcal M}) \leq \lambda ^+$
. We mostly work in the final extension but once step back into an intermediate random extension. Let
$\mathfrak {b} (\in ^*_{\mathcal M}) \leq \lambda ^+$
. We mostly work in the final extension but once step back into an intermediate random extension. Let
![]() $\{ x_\alpha \; | \; \alpha < \kappa \}$
list all reals. Let
$\{ x_\alpha \; | \; \alpha < \kappa \}$
list all reals. Let
![]() $\{ (A_\alpha , M_\alpha ) \; | \; \alpha < \kappa \}$
list all pairs
$\{ (A_\alpha , M_\alpha ) \; | \; \alpha < \kappa \}$
list all pairs
![]() $(A,M)$
such that
$(A,M)$
such that
![]() $A \in [\lambda ^+]^{\aleph _1}$
and M is a Borel meager set. Note that by our assumption
$A \in [\lambda ^+]^{\aleph _1}$
and M is a Borel meager set. Note that by our assumption
![]() $(\lambda ^+)^{\aleph _1} \leq \kappa ^{\aleph _1} = \kappa $
, so this is possible. Also let
$(\lambda ^+)^{\aleph _1} \leq \kappa ^{\aleph _1} = \kappa $
, so this is possible. Also let
![]() $\{ y_\xi \; | \; \xi < \omega _1 \} \subseteq \omega ^\omega $
be a sequence witnessing
$\{ y_\xi \; | \; \xi < \omega _1 \} \subseteq \omega ^\omega $
be a sequence witnessing
![]() $\mathfrak {b} (\in ^*) = \aleph _1$
.
$\mathfrak {b} (\in ^*) = \aleph _1$
.
Now construct functions
![]() $\{ f_\gamma \; | \; \gamma < \lambda ^+ \} \subseteq (\omega ^\omega )^{\omega ^\omega }$
and a strictly increasing sequence
$\{ f_\gamma \; | \; \gamma < \lambda ^+ \} \subseteq (\omega ^\omega )^{\omega ^\omega }$
and a strictly increasing sequence
![]() $\{ \zeta _\alpha \; | \; \alpha < \kappa \}$
of ordinals in
$\{ \zeta _\alpha \; | \; \alpha < \kappa \}$
of ordinals in
![]() $\kappa $
as follows. Suppose we are at step
$\kappa $
as follows. Suppose we are at step
![]() $\alpha $
. Find
$\alpha $
. Find
![]() $\zeta _\alpha $
such that
$\zeta _\alpha $
such that
-
•
 $\zeta _\alpha> \zeta _\beta $
for
$\zeta _\alpha> \zeta _\beta $
for
 $\beta < \alpha $
and
$\beta < \alpha $
and -
•
 $x_{\zeta _\alpha } \notin M_\alpha $
.
$x_{\zeta _\alpha } \notin M_\alpha $
.
Then define
![]() $f_\gamma (x_{\zeta _\alpha }) $
for
$f_\gamma (x_{\zeta _\alpha }) $
for
![]() $\gamma \in A_\alpha $
such that
$\gamma \in A_\alpha $
such that
Define the remaining values
![]() $f_\gamma (x_\beta )$
arbitrarily. This completes the construction of the
$f_\gamma (x_\beta )$
arbitrarily. This completes the construction of the
![]() $f_\gamma $
.
$f_\gamma $
.
We claim
![]() $\{ f_\gamma \; | \; \gamma < \lambda ^+ \}$
is a witness for
$\{ f_\gamma \; | \; \gamma < \lambda ^+ \}$
is a witness for
![]() $\mathfrak {b} (\in ^*_{\mathcal M})$
.
$\mathfrak {b} (\in ^*_{\mathcal M})$
.
For assume this were not the case. Then we could find
![]() $\varphi : \omega ^\omega \to \mathcal S$
such that
$\varphi : \omega ^\omega \to \mathcal S$
such that
for all
![]() $\gamma < \lambda ^+$
. For each such
$\gamma < \lambda ^+$
. For each such
![]() $\gamma $
let
$\gamma $
let
![]() $B_\gamma $
be a Borel meager set such that
$B_\gamma $
be a Borel meager set such that
There is a countable set
![]() $X_\gamma \subseteq \lambda $
such that the code of
$X_\gamma \subseteq \lambda $
such that the code of
![]() $B_\gamma $
lies in the
$B_\gamma $
lies in the
![]() $X_\gamma $
-extension (that is, the extension obtained by only adding the random reals with index in
$X_\gamma $
-extension (that is, the extension obtained by only adding the random reals with index in
![]() $X_\gamma $
). Note that
$X_\gamma $
). Note that
![]() ${\textrm {cof}} ( [ \lambda ]^{\leq \aleph _0} ) = \lambda $
.Footnote
1
Hence we can find a countable
${\textrm {cof}} ( [ \lambda ]^{\leq \aleph _0} ) = \lambda $
.Footnote
1
Hence we can find a countable
![]() $X \subseteq \lambda $
and a
$X \subseteq \lambda $
and a
![]() $Y \subseteq \lambda ^+$
of size
$Y \subseteq \lambda ^+$
of size
![]() $\lambda ^+$
s.t.
$\lambda ^+$
s.t.
![]() $X_\gamma \subseteq X$
for all
$X_\gamma \subseteq X$
for all
![]() $\gamma \in Y$
; in particular,
$\gamma \in Y$
; in particular,
![]() $B_\gamma $
is coded in the X-extension for all
$B_\gamma $
is coded in the X-extension for all
![]() $\gamma \in Y$
. We may assume Y also belongs to the X-extension. Let
$\gamma \in Y$
. We may assume Y also belongs to the X-extension. Let
![]() $A \subseteq Y$
be any subset of size
$A \subseteq Y$
be any subset of size
![]() $\aleph _1$
in the X-extension. Since
$\aleph _1$
in the X-extension. Since
![]() ${\textrm {add}} (\mathcal N) = {\textrm {add}} (\mathcal M) = \kappa = \mathfrak {c} \geq \aleph _2$
in the X-extension, the union
${\textrm {add}} (\mathcal N) = {\textrm {add}} (\mathcal M) = \kappa = \mathfrak {c} \geq \aleph _2$
in the X-extension, the union
![]() $\bigcup _{\gamma \in A} B_\gamma $
must be meager, so there is a Borel meager set M, still coded in the X-extension, such that
$\bigcup _{\gamma \in A} B_\gamma $
must be meager, so there is a Borel meager set M, still coded in the X-extension, such that
![]() $\bigcup _{\gamma \in A} B_\gamma \subseteq M$
. By construction, there is
$\bigcup _{\gamma \in A} B_\gamma \subseteq M$
. By construction, there is
![]() $\alpha < \kappa $
such that
$\alpha < \kappa $
such that
![]() $(A,M) = (A_\alpha , M_\alpha )$
. Since
$(A,M) = (A_\alpha , M_\alpha )$
. Since
![]() $x_{\zeta _\alpha } \notin M_\alpha $
we must have
$x_{\zeta _\alpha } \notin M_\alpha $
we must have
for all
![]() $\gamma \in A_\alpha $
. This clearly contradicts the fact that
$\gamma \in A_\alpha $
. This clearly contradicts the fact that
is a witness for
![]() $\mathfrak {b} (\in ^*)$
, and the proof of the theorem is complete.
$\mathfrak {b} (\in ^*)$
, and the proof of the theorem is complete.
4.6 The random/Hechler model
The random/Hechler model refers to the finite support iteration of length
![]() $\kappa $
which results from alternating between adding random reals and Hechler reals.
$\kappa $
which results from alternating between adding random reals and Hechler reals.
Theorem 4.10. In the random/Hechler model the following equalities hold.
-
(1) For all
 $\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
we have
$\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
we have
 $\mathfrak b(\in ^*_{\mathcal I}) = \aleph _1$
.
$\mathfrak b(\in ^*_{\mathcal I}) = \aleph _1$
. -
(2) All other cardinals of the form
 $\mathfrak b(R_{\mathcal I})$
are equal to
$\mathfrak b(R_{\mathcal I})$
are equal to
 $\kappa ^+$
.
$\kappa ^+$
.
Proof The values of the Cichoń diagram in the random/Hechler model are that all cardinals are
![]() $\kappa $
with the exception of
$\kappa $
with the exception of
![]() ${\textrm {add}} (\mathcal N) = \mathfrak b(\in ^*) = \aleph _1$
. It follows from Lemma 3.2 that
${\textrm {add}} (\mathcal N) = \mathfrak b(\in ^*) = \aleph _1$
. It follows from Lemma 3.2 that
![]() $\mathfrak b(\in ^*) = \mathfrak b(\in ^*_{\mathcal I}) = \aleph _1$
for all
$\mathfrak b(\in ^*) = \mathfrak b(\in ^*_{\mathcal I}) = \aleph _1$
for all
![]() $\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
and from Lemma 3.1 that all the other cardinals are
$\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
and from Lemma 3.1 that all the other cardinals are
![]() $\kappa ^+$
.
$\kappa ^+$
.
4.7 The eventually different model
Recall that eventually different forcing
![]() $\mathbb {E}$
consists of pairs
$\mathbb {E}$
consists of pairs
![]() $(s, E)$
so that
$(s, E)$
so that
![]() $s \in \omega ^{<\omega }$
and
$s \in \omega ^{<\omega }$
and
![]() $E \subseteq \omega ^\omega $
is finite. The extension relation is
$E \subseteq \omega ^\omega $
is finite. The extension relation is
![]() $(s_0, E_0) \leq (s_1, E_1)$
just in case
$(s_0, E_0) \leq (s_1, E_1)$
just in case
![]() $s_0 \supseteq s_1$
,
$s_0 \supseteq s_1$
,
![]() $E_0 \supseteq E_1$
and for all
$E_0 \supseteq E_1$
and for all
![]() $k \in {\textrm {dom}}(s_0) \setminus {\textrm {dom}}(s_1)$
we have
$k \in {\textrm {dom}}(s_0) \setminus {\textrm {dom}}(s_1)$
we have
![]() $s_0(k) \neq f(k)$
for all
$s_0(k) \neq f(k)$
for all
![]() $f \in E_1$
. The eventually different model is the model obtained by adding
$f \in E_1$
. The eventually different model is the model obtained by adding
![]() $\kappa $
-many eventually different reals with finite support over a model
$\kappa $
-many eventually different reals with finite support over a model
![]() $\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.5.6, p. 385].
$\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.5.6, p. 385].
Theorem 4.11. In the eventually different model the following equalities hold.
-
(1) For R equal to
 $\in ^*$
or
$\in ^*$
or
 $\leq ^*$
we have that
$\leq ^*$
we have that
 $\mathfrak b(R_{\mathcal M}) = \mathfrak b(R_{\mathcal K}) = \aleph _1$
.
$\mathfrak b(R_{\mathcal M}) = \mathfrak b(R_{\mathcal K}) = \aleph _1$
. -
(2)
 $\mathfrak b(\neq ^*_{\mathcal M}) = \kappa ^+$
.
$\mathfrak b(\neq ^*_{\mathcal M}) = \kappa ^+$
. -
(3)
 $\mathfrak b(\neq ^*_{\mathcal K}) = \kappa $
.
$\mathfrak b(\neq ^*_{\mathcal K}) = \kappa $
. -
(4) For all
 $R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
 $\mathfrak b(R_{\mathcal N}) = \kappa ^+$
.
$\mathfrak b(R_{\mathcal N}) = \kappa ^+$
.
Proof Recall that the values of the Cichoń diagram in the eventually different model are determined by
![]() $\mathfrak b = {\textrm {cov}}(\mathcal N) = \aleph _1$
and
$\mathfrak b = {\textrm {cov}}(\mathcal N) = \aleph _1$
and
![]() ${\textrm {non}}(\mathcal M) = \mathfrak b(\neq ^*) = {\textrm {cov}}(\mathcal M) = \kappa $
. From this item 1 follows from Lemma 3.2 and item 2 follows from Lemma 3.1. The third item follows from Lemma 1.4 since
${\textrm {non}}(\mathcal M) = \mathfrak b(\neq ^*) = {\textrm {cov}}(\mathcal M) = \kappa $
. From this item 1 follows from Lemma 3.2 and item 2 follows from Lemma 3.1. The third item follows from Lemma 1.4 since
![]() $\mathfrak b(\neq ^*) = \kappa $
and
$\mathfrak b(\neq ^*) = \kappa $
and
![]() ${\textrm {non}} (\mathcal K) = \mathfrak b = \aleph _1$
. The fourth item is verbatim the same as the proof that
${\textrm {non}} (\mathcal K) = \mathfrak b = \aleph _1$
. The fourth item is verbatim the same as the proof that
![]() $\mathfrak b(\in ^*_{\mathcal N}) = \kappa ^+$
holds in the Hechler model, see Theorem 4.5. This follows from the observation made after that proof plus the fact that
$\mathfrak b(\in ^*_{\mathcal N}) = \kappa ^+$
holds in the Hechler model, see Theorem 4.5. This follows from the observation made after that proof plus the fact that
![]() $\mathbb E$
is
$\mathbb E$
is
![]() $\sigma $
-centered and adds Cohen reals.
$\sigma $
-centered and adds Cohen reals.
4.8 The Laver model
The Laver model is the
![]() $\aleph _2$
length countable support iteration of Laver forcing over a model of
$\aleph _2$
length countable support iteration of Laver forcing over a model of
![]() $\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.6.13, p. 396].
$\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.6.13, p. 396].
Theorem 4.12. In the Laver model the following hold.
-
(1) For R equal to
 $\leq ^*$
or
$\leq ^*$
or
 $\neq ^*$
we have
$\neq ^*$
we have
 $\mathfrak b(R_{\mathcal K}) = \mathfrak b(R_{\mathcal M}) = \aleph _3$
.
$\mathfrak b(R_{\mathcal K}) = \mathfrak b(R_{\mathcal M}) = \aleph _3$
. -
(2) For all
 $R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
 $\mathfrak b(R_{\mathcal N}) = \aleph _2$
.
$\mathfrak b(R_{\mathcal N}) = \aleph _2$
. -
(3)
 $\mathfrak b(\in ^*_{\mathcal K}) = \aleph _1$
.
$\mathfrak b(\in ^*_{\mathcal K}) = \aleph _1$
.
Note that the one cardinal not determined by this theorem is
![]() $\mathfrak b(\in ^*_{\mathcal M})$
. This is the one cardinal that we were not able to calculate in one of the “standard iterated models.” By the fact that
$\mathfrak b(\in ^*_{\mathcal M})$
. This is the one cardinal that we were not able to calculate in one of the “standard iterated models.” By the fact that
![]() ${\textrm {cov}}(\mathcal M) = \aleph _1$
in the Laver model, Lemma 3.3 implies the value is either
${\textrm {cov}}(\mathcal M) = \aleph _1$
in the Laver model, Lemma 3.3 implies the value is either
![]() $\aleph _2$
or
$\aleph _2$
or
![]() $\aleph _3$
but we do not know which one. To show that it is
$\aleph _3$
but we do not know which one. To show that it is
![]() $\aleph _3$
it would suffice to exhibit an
$\aleph _3$
it would suffice to exhibit an
![]() $(\aleph _3, \aleph _1)$
-Rothberger family for
$(\aleph _3, \aleph _1)$
-Rothberger family for
![]() $\mathcal M$
however we do not know if one exists in the Laver model.
$\mathcal M$
however we do not know if one exists in the Laver model.
Proof Recall that the values of the Cichoń diagram in the Laver model are determined by
![]() ${\textrm {cov}}(\mathcal N) = {\textrm {non}}(\mathcal N) = \aleph _1$
and
${\textrm {cov}}(\mathcal N) = {\textrm {non}}(\mathcal N) = \aleph _1$
and
![]() $\mathfrak b = \aleph _2$
. Let
$\mathfrak b = \aleph _2$
. Let
![]() $\vec {l} = \{l_\alpha \; | \; \alpha < \aleph _2\}$
enumerate the Laver reals added and work in
$\vec {l} = \{l_\alpha \; | \; \alpha < \aleph _2\}$
enumerate the Laver reals added and work in
![]() $V[\vec {l}]$
. The first item then follows from Lemma 3.1. For the second item, the lower bound comes from Lemma 3.3. For the upper bound, observe that by Lemma 1.4 we have
$V[\vec {l}]$
. The first item then follows from Lemma 3.1. For the second item, the lower bound comes from Lemma 3.3. For the upper bound, observe that by Lemma 1.4 we have
![]() $\mathfrak b(\neq ^*_{\mathcal N}) \leq \mathfrak b(\neq ^*)^{{\textrm {non}}(\mathcal N)} = \aleph _2^{\aleph _1} = \aleph _2$
. The third item follows from Lemma 3.2, recalling that
$\mathfrak b(\neq ^*_{\mathcal N}) \leq \mathfrak b(\neq ^*)^{{\textrm {non}}(\mathcal N)} = \aleph _2^{\aleph _1} = \aleph _2$
. The third item follows from Lemma 3.2, recalling that
![]() ${\textrm {cov}}(\mathcal K) = \mathfrak {d}$
which is
${\textrm {cov}}(\mathcal K) = \mathfrak {d}$
which is
![]() $\aleph _2$
in the Laver model.
$\aleph _2$
in the Laver model.
4.9 The Miller model
The Miller model is the
![]() $\aleph _2$
-length countable support iteration of Miller forcing over a model of
$\aleph _2$
-length countable support iteration of Miller forcing over a model of
![]() $\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.5.2, p. 382].
$\mathsf {GCH}$
, see [Reference Bartoszyński and Judah1, Model 7.5.2, p. 382].
Theorem 4.13. In the Miller model the following hold.
-
(1) For all
 $R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
 $\mathfrak b(R_{\mathcal M}) = \mathfrak b(R_{\mathcal N}) =\aleph _2$
.
$\mathfrak b(R_{\mathcal M}) = \mathfrak b(R_{\mathcal N}) =\aleph _2$
. -
(2) For all
 $R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
we have
 $\mathfrak b(R_{\mathcal K}) = \aleph _1$
.
$\mathfrak b(R_{\mathcal K}) = \aleph _1$
.
Proof Recall that the values of the Cichoń diagram in the Miller model are determined by
![]() $\mathfrak {d} = \aleph _2$
and
$\mathfrak {d} = \aleph _2$
and
![]() ${\textrm {non}}(\mathcal N) = {\textrm {non}}(\mathcal M) = \aleph _1$
. The first item then follows by Lemmas 3.3 (for the lower bound) and 1.4 (for the upper bound). The second item follows from Lemma 3.2.
${\textrm {non}}(\mathcal N) = {\textrm {non}}(\mathcal M) = \aleph _1$
. The first item then follows by Lemmas 3.3 (for the lower bound) and 1.4 (for the upper bound). The second item follows from Lemma 3.2.
5
 $\mathsf {ZFC}$
results for the dominating numbers
$\mathsf {ZFC}$
results for the dominating numbers
In this section we explore
![]() $\mathsf {ZFC}$
provable equalities between the cardinals of the form
$\mathsf {ZFC}$
provable equalities between the cardinals of the form
![]() $\mathfrak {d}(R_{\mathcal I})$
. The main theorem of this section is the following, which shows that, unlike the bounding numbers,
$\mathfrak {d}(R_{\mathcal I})$
. The main theorem of this section is the following, which shows that, unlike the bounding numbers,
![]() $\mathfrak {d}(R_{\mathcal I})$
does not depend on
$\mathfrak {d}(R_{\mathcal I})$
does not depend on
![]() $\mathcal I$
. Note that this strengthens Main Theorem 1.4 and provides a proof of that theorem. We also investigate the relationship between the
$\mathcal I$
. Note that this strengthens Main Theorem 1.4 and provides a proof of that theorem. We also investigate the relationship between the
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
cardinals and the cardinals
$\mathfrak {d}(R_{\{\emptyset \}})$
cardinals and the cardinals
![]() $\mathfrak {d}^\lambda _\kappa $
introduced in [Reference Brendle3].
$\mathfrak {d}^\lambda _\kappa $
introduced in [Reference Brendle3].
Theorem 5.1. Assume
![]() $\mathcal I$
is an ideal on
$\mathcal I$
is an ideal on
![]() $\omega ^\omega $
so that
$\omega ^\omega $
so that
![]() $\mathrm{cof}(\mathcal I) \leq \mathfrak {c}$
and for all
$\mathrm{cof}(\mathcal I) \leq \mathfrak {c}$
and for all
![]() $X \in \mathcal I, |\omega ^\omega \setminus X| = \mathfrak {c}$
. Then
$X \in \mathcal I, |\omega ^\omega \setminus X| = \mathfrak {c}$
. Then
![]() $\mathfrak {d}(R_{\mathcal I}) = \mathfrak {d}(R_{\{\emptyset \}})$
for all
$\mathfrak {d}(R_{\mathcal I}) = \mathfrak {d}(R_{\{\emptyset \}})$
for all
![]() $R \in \{\in ^*, \leq ^*, \neq ^*\}$
. Here
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
. Here
![]() $\{\emptyset \}$
is the trivial ideal consisting only of the empty set.
$\{\emptyset \}$
is the trivial ideal consisting only of the empty set.
Note that
![]() $\mathcal N$
,
$\mathcal N$
,
![]() $\mathcal M$
and
$\mathcal M$
and
![]() $\mathcal K$
all fulfill the hypotheses on
$\mathcal K$
all fulfill the hypotheses on
![]() $\mathcal I$
in the theorem statement. This theorem is somewhat analogous to the fact that, e.g., the dominating number (on
$\mathcal I$
in the theorem statement. This theorem is somewhat analogous to the fact that, e.g., the dominating number (on
![]() $\omega $
) is unchanged if we insist on everywhere dominating versus mod finite domination. Note that there as well this fact does not hold true of unbounded sets.
$\omega $
) is unchanged if we insist on everywhere dominating versus mod finite domination. Note that there as well this fact does not hold true of unbounded sets.
Proof Fix an ideal
![]() $\mathcal I$
as in the statement of the theorem. Clearly any
$\mathcal I$
as in the statement of the theorem. Clearly any
![]() $R_{\{\emptyset \}}$
-dominating family is
$R_{\{\emptyset \}}$
-dominating family is
![]() $R_{\mathcal I}$
-dominating hence
$R_{\mathcal I}$
-dominating hence
![]() $\mathfrak {d}(R_{\mathcal I}) \leq \mathfrak {d} (R_{\{\emptyset \}})$
so we need to just prove the reverse inequality. Fix
$\mathfrak {d}(R_{\mathcal I}) \leq \mathfrak {d} (R_{\{\emptyset \}})$
so we need to just prove the reverse inequality. Fix
![]() $\kappa < \mathfrak {d}(R_{\{\emptyset \}})$
and a family of
$\kappa < \mathfrak {d}(R_{\{\emptyset \}})$
and a family of
![]() $\kappa $
many functions
$\kappa $
many functions
![]() $\mathcal F = \{f_\alpha \; | \; \alpha < \kappa \}$
. We need to see that
$\mathcal F = \{f_\alpha \; | \; \alpha < \kappa \}$
. We need to see that
![]() $\mathcal F$
is not dominating.
$\mathcal F$
is not dominating.
Enumerate (possibly with repetitions) a cofinal family in
![]() $\mathcal I$
,
$\mathcal I$
,
![]() $\{X_\alpha \; | \; \alpha < 2^{\aleph _0}\}$
. Also, let
$\{X_\alpha \; | \; \alpha < 2^{\aleph _0}\}$
. Also, let
![]() $\bar {\gamma }:2^{\aleph _0} \times 2^{\aleph _0} \to 2^{\aleph _0}$
be a bijection. Inductively on
$\bar {\gamma }:2^{\aleph _0} \times 2^{\aleph _0} \to 2^{\aleph _0}$
be a bijection. Inductively on
![]() $\gamma < 2^{\aleph _0}$
for
$\gamma < 2^{\aleph _0}$
for
![]() $\gamma = \bar {\gamma }(\alpha , \beta )$
define
$\gamma = \bar {\gamma }(\alpha , \beta )$
define
![]() $y_{\alpha , \beta } \in \omega ^\omega $
so that
$y_{\alpha , \beta } \in \omega ^\omega $
so that
![]() $y_{\alpha , \beta } \neq y_{\alpha ' , \beta '}$
for
$y_{\alpha , \beta } \neq y_{\alpha ' , \beta '}$
for
![]() $(\alpha , \beta ) \neq (\alpha ', \beta ' )$
and
$(\alpha , \beta ) \neq (\alpha ', \beta ' )$
and
![]() $y_{\alpha , \beta } \notin X_\alpha $
for all
$y_{\alpha , \beta } \notin X_\alpha $
for all
![]() $\beta < 2^{\aleph _0}$
. Note that this is possible by the assumption that
$\beta < 2^{\aleph _0}$
. Note that this is possible by the assumption that
![]() $\omega ^\omega \setminus X_\alpha $
has size continuum for all
$\omega ^\omega \setminus X_\alpha $
has size continuum for all
![]() $\alpha $
.
$\alpha $
.
For each
![]() $\alpha < 2^{\aleph _0}$
consider the restriction of
$\alpha < 2^{\aleph _0}$
consider the restriction of
![]() $\mathcal F$
to
$\mathcal F$
to
![]() $\{y_{\alpha , \beta } \; | \; \beta < 2^{\aleph _0}\}$
, i.e.,
$\{y_{\alpha , \beta } \; | \; \beta < 2^{\aleph _0}\}$
, i.e.,
![]() $\{f_\gamma \upharpoonright \{y_{\alpha , \beta } \; | \; \beta < 2^{\aleph _0}\} \; | \; f_\gamma \in \mathcal F\}$
. Since
$\{f_\gamma \upharpoonright \{y_{\alpha , \beta } \; | \; \beta < 2^{\aleph _0}\} \; | \; f_\gamma \in \mathcal F\}$
. Since
![]() $\kappa < \mathfrak {d} (R_{\{\emptyset \}})$
, none of these sets are dominating so there is a
$\kappa < \mathfrak {d} (R_{\{\emptyset \}})$
, none of these sets are dominating so there is a
![]() $g:\omega ^\omega \to \omega ^\omega $
so that for all
$g:\omega ^\omega \to \omega ^\omega $
so that for all
![]() $f \in \mathcal F$
and all
$f \in \mathcal F$
and all
![]() $\alpha < 2^{\aleph _0}$
there is a
$\alpha < 2^{\aleph _0}$
there is a
![]() $\beta $
so that
$\beta $
so that
![]() $\neg (g(y_{\alpha , \beta }) \mathbin{R} f (y_{\alpha , \beta }))$
. But since the
$\neg (g(y_{\alpha , \beta }) \mathbin{R} f (y_{\alpha , \beta }))$
. But since the
![]() $X_\alpha $
’s formed a basis for
$X_\alpha $
’s formed a basis for
![]() $\mathcal I$
it follows that g is not
$\mathcal I$
it follows that g is not
![]() $R_{\mathcal I}$
-bounded by any
$R_{\mathcal I}$
-bounded by any
![]() $f \in \mathcal F$
, as needed.
$f \in \mathcal F$
, as needed.
As a result of this theorem we have the following.
Corollary 5.2. For all R and
![]() $\mathcal I$
we have
$\mathcal I$
we have
![]() $\mathfrak {d}(R_{\mathcal I})> 2^{\aleph _0}$
.
$\mathfrak {d}(R_{\mathcal I})> 2^{\aleph _0}$
.
Proof In light of Theorem 5.1 it suffices to show that for all R,
![]() $\mathfrak {d}(R_{\{\emptyset \}} )> 2^{\aleph _0}$
. Fix a family
$\mathfrak {d}(R_{\{\emptyset \}} )> 2^{\aleph _0}$
. Fix a family
![]() $\mathcal F = \{f_\alpha \; | \; \alpha < 2^{\aleph _0}\} \subseteq (\omega ^\omega )^{\omega ^\omega }$
(or
$\mathcal F = \{f_\alpha \; | \; \alpha < 2^{\aleph _0}\} \subseteq (\omega ^\omega )^{\omega ^\omega }$
(or
![]() $\mathcal S^{\omega ^\omega }$
in the case of
$\mathcal S^{\omega ^\omega }$
in the case of
![]() $R = {\in}^*$
). Enumerate
$R = {\in}^*$
). Enumerate
![]() $\omega ^\omega $
as
$\omega ^\omega $
as
![]() $\{x_\alpha \; | \; \alpha < 2^{\aleph _0}\}$
. Define
$\{x_\alpha \; | \; \alpha < 2^{\aleph _0}\}$
. Define
![]() $g:\omega ^\omega \to \omega ^\omega $
so that
$g:\omega ^\omega \to \omega ^\omega $
so that
![]() $g(x_\alpha )$
is not R below
$g(x_\alpha )$
is not R below
![]() $f_\alpha (x_\alpha )$
. It follows that for each
$f_\alpha (x_\alpha )$
. It follows that for each
![]() $\alpha $
there is an x so that
$\alpha $
there is an x so that
![]() $\neg (g(x) \mathbin{R} f_\alpha (x))$
and hence
$\neg (g(x) \mathbin{R} f_\alpha (x))$
and hence
![]() $\mathcal F$
does not contain a bound on g so it is not dominating.
$\mathcal F$
does not contain a bound on g so it is not dominating.
In the next section we study consistent inequalities between the dominating numbers of the relations
![]() $R_{\mathcal I}$
. The computations of these cardinals in various models factor through relating the cardinals
$R_{\mathcal I}$
. The computations of these cardinals in various models factor through relating the cardinals
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
to the cardinals
$\mathfrak {d}(R_{\{\emptyset \}})$
to the cardinals
![]() $\mathfrak {d}_\kappa ^\lambda $
of [Reference Brendle3, Section 4]. In the rest of this section we establish
$\mathfrak {d}_\kappa ^\lambda $
of [Reference Brendle3, Section 4]. In the rest of this section we establish
![]() $\mathsf {ZFC}$
results between these two families of cardinals. Recall that if
$\mathsf {ZFC}$
results between these two families of cardinals. Recall that if
![]() $\lambda \geq \kappa $
and
$\lambda \geq \kappa $
and
![]() $f, g \in \kappa ^\lambda $
then we let
$f, g \in \kappa ^\lambda $
then we let
![]() $f \leq ^* g$
if and only if
$f \leq ^* g$
if and only if
![]() $\{\alpha < \lambda \; | \; f(\alpha )> g(\alpha )\}$
has size less than
$\{\alpha < \lambda \; | \; f(\alpha )> g(\alpha )\}$
has size less than
![]() $\kappa $
. The cardinal
$\kappa $
. The cardinal
![]() $\mathfrak {d}^\lambda _\kappa $
is the dominating number of this relation. The following, which was proved in [Reference Brendle3], will be useful for us.
$\mathfrak {d}^\lambda _\kappa $
is the dominating number of this relation. The following, which was proved in [Reference Brendle3], will be useful for us.
Fact 5.3. [Reference Brendle3, Proposition 12] The value of
![]() $\mathfrak {d}^\lambda _\kappa $
is unchanged if we work with the total domination relation as opposed to the mod
$\mathfrak {d}^\lambda _\kappa $
is unchanged if we work with the total domination relation as opposed to the mod
![]() ${<} \kappa $
domination.
${<} \kappa $
domination.
The main question, which is open, is whether every cardinal
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
is provably equal to a cardinal of the form
$\mathfrak {d}(R_{\{\emptyset \}})$
is provably equal to a cardinal of the form
![]() $\mathfrak {d}^\lambda _\kappa $
. Indeed, in every model we know the value of
$\mathfrak {d}^\lambda _\kappa $
. Indeed, in every model we know the value of
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
is equal to that of
$\mathfrak {d}(R_{\{\emptyset \}})$
is equal to that of
![]() $\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b(R)}$
. We know that this equality follows from certain extra assumptions about R. To explain this result we need a few more definitions.
$\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b(R)}$
. We know that this equality follows from certain extra assumptions about R. To explain this result we need a few more definitions.
Definition 5.4. Fix a relation
![]() $R \in \{\in ^*, \leq ^*, \neq ^*\}$
and an arbitrary cardinal
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
and an arbitrary cardinal
![]() $\kappa $
.
$\kappa $
.
-
(1) A family
 $\{x_\alpha \; | \; \alpha < \kappa \} \subseteq \omega ^\omega $
is an eventually R-dominating sequence if for all
$\{x_\alpha \; | \; \alpha < \kappa \} \subseteq \omega ^\omega $
is an eventually R-dominating sequence if for all
 $y \in \omega ^\omega $
there is an
$y \in \omega ^\omega $
there is an
 $\alpha _0 < \kappa $
so that for all
$\alpha _0 < \kappa $
so that for all
 $\alpha \in [\alpha _0, \kappa )$
,
$\alpha \in [\alpha _0, \kappa )$
,
 $y\mathbin{R}x_\alpha $
.
$y\mathbin{R}x_\alpha $
. -
(2) A family
 $\{x_\alpha \; | \; \alpha < \kappa \} \subseteq \omega ^\omega $
is an eventually R-unbounded sequence if for all
$\{x_\alpha \; | \; \alpha < \kappa \} \subseteq \omega ^\omega $
is an eventually R-unbounded sequence if for all
 $y \in \omega ^\omega $
there is an
$y \in \omega ^\omega $
there is an
 $\alpha _0 < \kappa $
so that for all
$\alpha _0 < \kappa $
so that for all
 $\alpha \in [\alpha _0, \kappa )$
,
$\alpha \in [\alpha _0, \kappa )$
,
 $\neg (x_\alpha \mathbin{R} y)$
.
$\neg (x_\alpha \mathbin{R} y)$
.
It is not hard to check that these two notions are dual to one another, i.e., R-eventually dominating is
![]() $\neg \check {R}$
-eventually unbounded where
$\neg \check {R}$
-eventually unbounded where
![]() $\neg \check {R}$
is the dual relation to R. Note also that the existence of an eventually R-dominating sequence of length
$\neg \check {R}$
is the dual relation to R. Note also that the existence of an eventually R-dominating sequence of length
![]() $\kappa $
implies that
$\kappa $
implies that
![]() $\mathfrak b(R) \geq cf(\kappa )$
and
$\mathfrak b(R) \geq cf(\kappa )$
and
![]() $\mathfrak {d}(R) \leq cf(\kappa )$
. Dually, the existence of an eventually R-unbounded sequence of length
$\mathfrak {d}(R) \leq cf(\kappa )$
. Dually, the existence of an eventually R-unbounded sequence of length
![]() $\kappa $
implies
$\kappa $
implies
![]() $\mathfrak b(R) \leq cf(\kappa )$
and
$\mathfrak b(R) \leq cf(\kappa )$
and
![]() $\mathfrak {d}(R) \geq cf(\kappa )$
. Some examples will be helpful also moving forward.
$\mathfrak {d}(R) \geq cf(\kappa )$
. Some examples will be helpful also moving forward.
Example 5.5.
-
(1) In
 $\mathsf {ZFC}$
there is an eventually
$\mathsf {ZFC}$
there is an eventually
 $\leq ^*$
-unbounded sequence of length
$\leq ^*$
-unbounded sequence of length
 $\mathfrak b$
. Meanwhile the existence of an eventually
$\mathfrak b$
. Meanwhile the existence of an eventually
 $\leq ^*$
-dominating sequence of length
$\leq ^*$
-dominating sequence of length
 $\kappa $
implies that
$\kappa $
implies that
 $\mathfrak b = \mathfrak {d} = cf(\kappa )$
. Conversely if
$\mathfrak b = \mathfrak {d} = cf(\kappa )$
. Conversely if
 $\mathfrak b = \mathfrak {d} = \kappa $
then there is an eventually
$\mathfrak b = \mathfrak {d} = \kappa $
then there is an eventually
 $\leq ^*$
-dominating sequence of length
$\leq ^*$
-dominating sequence of length
 $\kappa $
.
$\kappa $
. -
(2) In the Cohen model there are eventually
 $\neq ^*$
-unbounded sequences of length
$\neq ^*$
-unbounded sequences of length
 $\kappa $
for
$\kappa $
for
 $\aleph _1 \leq \kappa \leq \mathfrak {c}$
but no eventually
$\aleph _1 \leq \kappa \leq \mathfrak {c}$
but no eventually
 $\neq ^*$
-dominating sequences of any length.
$\neq ^*$
-dominating sequences of any length. -
(3) In the random model there are eventually
 $\neq ^*$
-dominating sequences of length
$\neq ^*$
-dominating sequences of length
 $\kappa $
for
$\kappa $
for
 $\aleph _1 \leq \kappa \leq \mathfrak {c}$
but no eventually
$\aleph _1 \leq \kappa \leq \mathfrak {c}$
but no eventually
 $\neq ^*$
-unbounded sequences of any length.
$\neq ^*$
-unbounded sequences of any length.
Lemma 5.6. Fix
![]() $R \in \{\in ^*, \leq ^*, \neq ^*\}$
and a cardinal
$R \in \{\in ^*, \leq ^*, \neq ^*\}$
and a cardinal
![]() $\kappa \leq \mathfrak {c}$
.
$\kappa \leq \mathfrak {c}$
.
-
(1) If there is an eventually R-dominating sequence of length
 $\kappa $
then
$\kappa $
then
 $\mathfrak {d}(R_{\{\emptyset \}}) \leq \mathfrak {d}^{\mathfrak {c}}_{\kappa }$
.
$\mathfrak {d}(R_{\{\emptyset \}}) \leq \mathfrak {d}^{\mathfrak {c}}_{\kappa }$
. -
(2) If there is an eventually R-unbounded sequence of length
 $\kappa $
then
$\kappa $
then
 $\mathfrak {d}(R_{\{\emptyset \}}) \geq \mathfrak {d}^{\mathfrak {c}}_{\kappa }$
.
$\mathfrak {d}(R_{\{\emptyset \}}) \geq \mathfrak {d}^{\mathfrak {c}}_{\kappa }$
.
Proof Let
![]() $\mathcal F = \{x_\alpha \; | \; \alpha < \kappa \} \subseteq \omega ^\omega $
be an eventually R-dominating sequence of length
$\mathcal F = \{x_\alpha \; | \; \alpha < \kappa \} \subseteq \omega ^\omega $
be an eventually R-dominating sequence of length
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\mathcal G$
be a witness for
$\mathcal G$
be a witness for
![]() $\mathfrak {d}^{\mathfrak {c}}_\kappa $
. Also let
$\mathfrak {d}^{\mathfrak {c}}_\kappa $
. Also let
![]() $\{y_\gamma \; | \; \gamma < \mathfrak {c}\}$
enumerate
$\{y_\gamma \; | \; \gamma < \mathfrak {c}\}$
enumerate
![]() $\omega ^\omega $
. For
$\omega ^\omega $
. For
![]() $g \in \mathcal G$
define
$g \in \mathcal G$
define
![]() $g' \in (\omega ^\omega )^{\omega ^\omega }$
so that
$g' \in (\omega ^\omega )^{\omega ^\omega }$
so that
![]() $g'(y_\gamma ) = x_{g(\gamma )}$
. It follows that
$g'(y_\gamma ) = x_{g(\gamma )}$
. It follows that
![]() $\mathcal G ' =\{g' \; | \; g \in \mathcal G\}$
is a
$\mathcal G ' =\{g' \; | \; g \in \mathcal G\}$
is a
![]() $R_{\{\emptyset \}}$
-dominating family, as needed.
$R_{\{\emptyset \}}$
-dominating family, as needed.
The second item is proved the same way by duality.
As a corollary of this lemma we have the following in the case that
![]() $R = {\leq}^*$
. Note that this relation is particularly nice because it is a partial order (when moded out by equality “mod finite”) and hence there is in
$R = {\leq}^*$
. Note that this relation is particularly nice because it is a partial order (when moded out by equality “mod finite”) and hence there is in
![]() $\mathsf {ZFC}$
an eventually
$\mathsf {ZFC}$
an eventually
![]() $\leq ^*$
-unbounded family of size
$\leq ^*$
-unbounded family of size
![]() $\mathfrak b$
and therefore
$\mathfrak b$
and therefore
![]() $\mathfrak {d}(\leq ^*_{\{\emptyset \}}) \geq \mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
.
$\mathfrak {d}(\leq ^*_{\{\emptyset \}}) \geq \mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
.
Lemma 5.7. If
![]() $\mathfrak b = \mathfrak {d}$
then
$\mathfrak b = \mathfrak {d}$
then
![]() $\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
.
$\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
.
Proof If
![]() $\mathfrak b = \mathfrak {d}$
there is a scale of length
$\mathfrak b = \mathfrak {d}$
there is a scale of length
![]() $\mathfrak b$
, i.e., a dominating family well-ordered by
$\mathfrak b$
, i.e., a dominating family well-ordered by
![]() $\leq ^*$
of length
$\leq ^*$
of length
![]() $\mathfrak b$
, see [Reference Blass, Foreman and Kanamori2, Theorem 2.6]. Such a scale is simultaneously an eventually
$\mathfrak b$
, see [Reference Blass, Foreman and Kanamori2, Theorem 2.6]. Such a scale is simultaneously an eventually
![]() $\leq ^*$
-unbounded and an eventually
$\leq ^*$
-unbounded and an eventually
![]() $\leq ^*$
-dominating sequence. Hence, by combining the first and second items in Lemma 5.6 it follows that
$\leq ^*$
-dominating sequence. Hence, by combining the first and second items in Lemma 5.6 it follows that
![]() $\mathfrak {d}(R_{\emptyset \}})$
is equal to
$\mathfrak {d}(R_{\emptyset \}})$
is equal to
![]() $\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
.
$\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
.
It is unclear whether similar hypotheses to
![]() $\mathfrak b = \mathfrak {d}$
imply the same for the other relations. It is also unclear if the additional assumption is necessary. In every model we have computed
$\mathfrak b = \mathfrak {d}$
imply the same for the other relations. It is also unclear if the additional assumption is necessary. In every model we have computed
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
, regardless of whether or not
$\mathfrak {d}(R_{\{\emptyset \}})$
, regardless of whether or not
![]() $\mathfrak b = \mathfrak {d}$
, we have equality. We conjecture this is a
$\mathfrak b = \mathfrak {d}$
, we have equality. We conjecture this is a
![]() $\mathsf {ZFC}$
phenomenon.
$\mathsf {ZFC}$
phenomenon.
Conjecture 5.1. In
![]() $\mathsf {ZFC}$
it is provable that
$\mathsf {ZFC}$
it is provable that
![]() $\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b} = \mathfrak {d}(\leq ^*_{\{\emptyset \}})$
.
$\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b} = \mathfrak {d}(\leq ^*_{\{\emptyset \}})$
.
This conjecture is true if
![]() $\mathfrak {c} < \aleph _\omega $
.
$\mathfrak {c} < \aleph _\omega $
.
Theorem 5.8. If
![]() $\mathfrak {c} = \mathfrak b^{+n}$
for some
$\mathfrak {c} = \mathfrak b^{+n}$
for some
![]() $n < \omega $
then
$n < \omega $
then
![]() $\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b} = \mathfrak {d}(\leq ^*_{\{\emptyset \}})$
.
$\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b} = \mathfrak {d}(\leq ^*_{\{\emptyset \}})$
.
Proof Let M be a model of a large enough fragment of
![]() $\mathsf {ZFC}$
of size
$\mathsf {ZFC}$
of size
![]() $\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
containing a witness for
$\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
containing a witness for
![]() $\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
. We show that M contains a witness for
$\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b}$
. We show that M contains a witness for
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
as well. Since the
$\mathfrak {d}(R_{\{\emptyset \}})$
as well. Since the
![]() $\mathfrak {d}^{\mathfrak {c}}_\kappa $
are decreasing in
$\mathfrak {d}^{\mathfrak {c}}_\kappa $
are decreasing in
![]() $\kappa $
(at least at successor steps), see [Reference Brendle3, Theorem 13], we may assume that M also contains a witness for each
$\kappa $
(at least at successor steps), see [Reference Brendle3, Theorem 13], we may assume that M also contains a witness for each
![]() $\mathfrak {d}^{\mathfrak {c}}_\kappa $
for
$\mathfrak {d}^{\mathfrak {c}}_\kappa $
for
![]() $\mathfrak b \leq \kappa \leq \mathfrak {c}$
. Note that
$\mathfrak b \leq \kappa \leq \mathfrak {c}$
. Note that
![]() $\omega ^\omega \subseteq M$
. Let
$\omega ^\omega \subseteq M$
. Let
![]() $\{y_\gamma \; | \; \gamma < \mathfrak {c}\} \in M$
enumerate
$\{y_\gamma \; | \; \gamma < \mathfrak {c}\} \in M$
enumerate
![]() $\omega ^\omega $
. By induction on
$\omega ^\omega $
. By induction on
![]() $\kappa $
we show the following:
$\kappa $
we show the following:
-
(*): For any
 $\kappa \in [\mathfrak b, \mathfrak {c}]$
if
$\kappa \in [\mathfrak b, \mathfrak {c}]$
if
 $\{x_{\gamma , \alpha } \; | \; \gamma < \mathfrak {c}, \alpha < \kappa \} \in M$
is a list of reals and
$\{x_{\gamma , \alpha } \; | \; \gamma < \mathfrak {c}, \alpha < \kappa \} \in M$
is a list of reals and
 $f:\mathfrak {c} \to \kappa $
is arbitrary, then there is a
$f:\mathfrak {c} \to \kappa $
is arbitrary, then there is a
 $g:\omega ^\omega \to \omega ^\omega $
in M so that for a
$g:\omega ^\omega \to \omega ^\omega $
in M so that for a
 $\gamma < \mathfrak {c}$
,
$\gamma < \mathfrak {c}$
,
 $x_{\gamma , f(\gamma )} \leq ^* g(y_\gamma )$
.
$x_{\gamma , f(\gamma )} \leq ^* g(y_\gamma )$
.
This is clearly true for
![]() $\kappa = \mathfrak b$
. Furthermore if
$\kappa = \mathfrak b$
. Furthermore if
![]() $(*)$
holds for
$(*)$
holds for
![]() $\kappa = \mathfrak {c}$
we’re done. Therefore assume
$\kappa = \mathfrak {c}$
we’re done. Therefore assume
![]() $(*)$
holds for
$(*)$
holds for
![]() $\kappa $
and we will show it holds for
$\kappa $
and we will show it holds for
![]() $\kappa ^+$
. Let
$\kappa ^+$
. Let
![]() $\{x_{\gamma , \alpha } \; | \; \gamma < \mathfrak {c}, \alpha < \kappa ^+\} \in M$
be a list of reals. Let
$\{x_{\gamma , \alpha } \; | \; \gamma < \mathfrak {c}, \alpha < \kappa ^+\} \in M$
be a list of reals. Let
![]() $f:\mathfrak {c} \to \kappa ^+$
be arbitrary and let
$f:\mathfrak {c} \to \kappa ^+$
be arbitrary and let
![]() $h:\mathfrak {c} \to \kappa ^+$
in M dominate f everywhere. Reindex the list in M so that for each
$h:\mathfrak {c} \to \kappa ^+$
in M dominate f everywhere. Reindex the list in M so that for each
![]() $\gamma $
we have
$\gamma $
we have
![]() $\{x^{\prime }_{\gamma , \alpha } \; | \; \alpha < \kappa \} = \{x_{\gamma , \alpha }\; | \; \alpha < h(\gamma )\}$
. Applying the induction hypothesis to
$\{x^{\prime }_{\gamma , \alpha } \; | \; \alpha < \kappa \} = \{x_{\gamma , \alpha }\; | \; \alpha < h(\gamma )\}$
. Applying the induction hypothesis to
![]() $\{x^{\prime }_{\gamma , \alpha } \; | \; \gamma < \mathfrak {c}, \alpha < \kappa \} \in M$
and
$\{x^{\prime }_{\gamma , \alpha } \; | \; \gamma < \mathfrak {c}, \alpha < \kappa \} \in M$
and
![]() $f':\mathfrak {c} \to \kappa $
given by
$f':\mathfrak {c} \to \kappa $
given by
![]() $x^{\prime }_{\gamma , f'(\gamma )} = x_{\gamma , f(\gamma )}$
gives an
$x^{\prime }_{\gamma , f'(\gamma )} = x_{\gamma , f(\gamma )}$
gives an
![]() $g \in M$
so that for all
$g \in M$
so that for all
![]() $\gamma < \mathfrak {c}$
,
$\gamma < \mathfrak {c}$
,
![]() $x^{\prime }_{\gamma , f'(\gamma )} = x_{\gamma , f(\gamma )} \leq ^* g(y_\gamma )$
as needed.
$x^{\prime }_{\gamma , f'(\gamma )} = x_{\gamma , f(\gamma )} \leq ^* g(y_\gamma )$
as needed.
6 Consistency results for the dominating numbers
In this section we consider consistency results for the cardinals of the form
![]() $\mathfrak {d}(R_{\mathcal I})$
. As shown in Theorem 5.1 the ideal here is unimportant so we really only have three cardinals,
$\mathfrak {d}(R_{\mathcal I})$
. As shown in Theorem 5.1 the ideal here is unimportant so we really only have three cardinals,
![]() $\mathfrak {d}(\in ^*_{\{\emptyset \}})$
,
$\mathfrak {d}(\in ^*_{\{\emptyset \}})$
,
![]() $\mathfrak {d}(\leq ^*_{\{\emptyset \}})$
,
$\mathfrak {d}(\leq ^*_{\{\emptyset \}})$
,
![]() $\mathfrak {d}(\neq ^*_{\{\emptyset \}})$
. Nevertheless we can separate them all.
$\mathfrak {d}(\neq ^*_{\{\emptyset \}})$
. Nevertheless we can separate them all.
Theorem 6.1. The following constellations of cardinals are all consistent.
-
(1)
 $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) < \mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}(\in ^*_{\{\emptyset \}})$
.
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) < \mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}(\in ^*_{\{\emptyset \}})$
. -
(2)
 $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \mathfrak {d}(\leq ^*_{\{\emptyset \}}) < \mathfrak {d}(\in ^*_{\{\emptyset \}})$
.
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \mathfrak {d}(\leq ^*_{\{\emptyset \}}) < \mathfrak {d}(\in ^*_{\{\emptyset \}})$
. -
(3)
 $\mathfrak {d}(\neq ^*_{\{\emptyset \}})< \mathfrak {d}(\leq ^*_{\{\emptyset \}}) < \mathfrak {d}(\in ^*_{\{\emptyset \}})$
.
$\mathfrak {d}(\neq ^*_{\{\emptyset \}})< \mathfrak {d}(\leq ^*_{\{\emptyset \}}) < \mathfrak {d}(\in ^*_{\{\emptyset \}})$
. -
(4)
 $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}(\in ^*_{\{\emptyset \}}) < 2^{\mathfrak {c}}$
.
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}(\in ^*_{\{\emptyset \}}) < 2^{\mathfrak {c}}$
. -
(5)
 $\mathfrak {c}^+ < \mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}(\in ^*_{\{\emptyset \}})$
.
$\mathfrak {c}^+ < \mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}(\in ^*_{\{\emptyset \}})$
.
The models witnessing Theorem 6.1 are discussed in the proofs of Lemmas 6.5–6.7. The general form of proving these consistency results involves first adding Cohen subsets to
![]() $\omega _1$
and then adding various kinds of reals. The point will be that all of the
$\omega _1$
and then adding various kinds of reals. The point will be that all of the
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
cardinals will reduce to combinatorics on some space of the form
$\mathfrak {d}(R_{\{\emptyset \}})$
cardinals will reduce to combinatorics on some space of the form
![]() $\kappa ^{\mathfrak {c}}$
but depending on how many subsets of
$\kappa ^{\mathfrak {c}}$
but depending on how many subsets of
![]() $\omega $
and
$\omega $
and
![]() $\omega _1$
we add, as well as which type of reals we add,
$\omega _1$
we add, as well as which type of reals we add,
![]() $\kappa $
may change depending on the relation R. Towards proving these results, we begin with a simple, well known lemma.
$\kappa $
may change depending on the relation R. Towards proving these results, we begin with a simple, well known lemma.
Lemma 6.2. Assume
![]() $\mathsf {GCH}$
and let
$\mathsf {GCH}$
and let
![]() $\kappa> \aleph _3$
be a regular cardinal. Let
$\kappa> \aleph _3$
be a regular cardinal. Let
![]() $G \subseteq add(\omega _1, \kappa )$
be generic over V. Then in
$G \subseteq add(\omega _1, \kappa )$
be generic over V. Then in
![]() $V[G]$
we have that
$V[G]$
we have that
![]() $\mathfrak {d}_{\omega _1} = \kappa $
and
$\mathfrak {d}_{\omega _1} = \kappa $
and
![]() $\mathfrak {d}_{\omega _2} = \aleph _3$
.
$\mathfrak {d}_{\omega _2} = \aleph _3$
.
Proof The fact that
![]() $\mathfrak {d}_{\omega _1} = \kappa $
is well known, see for example [Reference Brendle, Brooke-Taylor, Friedman and Montoya4]. For
$\mathfrak {d}_{\omega _1} = \kappa $
is well known, see for example [Reference Brendle, Brooke-Taylor, Friedman and Montoya4]. For
![]() $\mathfrak {d}_{\omega _2}$
it suffices to note that, by the
$\mathfrak {d}_{\omega _2}$
it suffices to note that, by the
![]() $\aleph _2$
-c.c., the forcing is
$\aleph _2$
-c.c., the forcing is
![]() $\aleph _2^{\aleph _2}$
-bounding and hence the ground model functions
$\aleph _2^{\aleph _2}$
-bounding and hence the ground model functions
![]() $f:\aleph _2 \to \aleph _2$
form a dominating family.
$f:\aleph _2 \to \aleph _2$
form a dominating family.
We also will use the following result several times.
Lemma 6.3. Assume
![]() $\mathsf {GCH}$
. Fix
$\mathsf {GCH}$
. Fix
![]() $R \in \{\neq ^*, \leq ^*, \in ^*\}$
. Let
$R \in \{\neq ^*, \leq ^*, \in ^*\}$
. Let
![]() $G\subseteq add(\omega _1, \omega _4)$
be generic over V. In
$G\subseteq add(\omega _1, \omega _4)$
be generic over V. In
![]() $V[G]$
let
$V[G]$
let
![]() $\mathbb Q \in V$
be ccc (in
$\mathbb Q \in V$
be ccc (in
![]() $V[G]$
) and suppose
$V[G]$
) and suppose
![]() $\Vdash _{\mathbb Q}$
“
$\Vdash _{\mathbb Q}$
“
![]() $\mathfrak b(R) = \aleph _1$
and
$\mathfrak b(R) = \aleph _1$
and
![]() $2^{\aleph _0} = \aleph _2$
.” Let
$2^{\aleph _0} = \aleph _2$
.” Let
![]() $H \subseteq \mathbb Q$
be generic over
$H \subseteq \mathbb Q$
be generic over
![]() $V[G]$
. Then in
$V[G]$
. Then in
![]() $V[G][H]$
we have that
$V[G][H]$
we have that
![]() $\mathfrak {d}(R_{\{\emptyset \}}) = \aleph _4$
.
$\mathfrak {d}(R_{\{\emptyset \}}) = \aleph _4$
.
Proof First work in
![]() $V[G][H]$
and note that the cardinal arithmetic in this model is
$V[G][H]$
and note that the cardinal arithmetic in this model is
![]() $2^{\aleph _0} = \aleph _2$
and
$2^{\aleph _0} = \aleph _2$
and
![]() $2^{\aleph _1} = 2^{\aleph _2} = 2^{\aleph _3} = \aleph _4$
and by Lemma 6.2
$2^{\aleph _1} = 2^{\aleph _2} = 2^{\aleph _3} = \aleph _4$
and by Lemma 6.2
![]() $,\mathfrak {d}_{\aleph _1} = \aleph _4$
and
$,\mathfrak {d}_{\aleph _1} = \aleph _4$
and
![]() $\mathfrak {d}_{\aleph _2} = \aleph _3$
. It follows that every
$\mathfrak {d}_{\aleph _2} = \aleph _3$
. It follows that every
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
is either
$\mathfrak {d}(R_{\{\emptyset \}})$
is either
![]() $\aleph _3$
or
$\aleph _3$
or
![]() $\aleph _4$
in light of Corollary 5.2. Therefore to prove the lemma it suffices to show that
$\aleph _4$
in light of Corollary 5.2. Therefore to prove the lemma it suffices to show that
![]() $\mathfrak {d}(R_{\{\emptyset \}})> \aleph _3$
.
$\mathfrak {d}(R_{\{\emptyset \}})> \aleph _3$
.
Suppose towards a contradiction that
![]() $\{\dot {f}_\alpha \; |\; \alpha < \omega _3\}$
names a
$\{\dot {f}_\alpha \; |\; \alpha < \omega _3\}$
names a
![]() $R_{\{\emptyset \}}$
-dominating family in
$R_{\{\emptyset \}}$
-dominating family in
![]() $V[G][H]$
. Using the product lemma, plus properness, we can find an intermediate extension containing all of the
$V[G][H]$
. Using the product lemma, plus properness, we can find an intermediate extension containing all of the
![]() $\dot {f}_\alpha $
’s and H. Call this
$\dot {f}_\alpha $
’s and H. Call this
![]() $W\subseteq V[G][H]$
. By the ccc of
$W\subseteq V[G][H]$
. By the ccc of
![]() $\mathbb Q$
, the remainder forcing
$\mathbb Q$
, the remainder forcing
![]() $\mathbb R \in W$
is
$\mathbb R \in W$
is
![]() $\omega $
-distributive and, in fact, is isomorphic to
$\omega $
-distributive and, in fact, is isomorphic to
![]() $add(\omega _1, \omega _4)^V$
. Moreover we can assume that
$add(\omega _1, \omega _4)^V$
. Moreover we can assume that
![]() $W \models \mathfrak b(R) = \aleph _1$
since this is true in the final model so we can add the unbounded family. Fix an
$W \models \mathfrak b(R) = \aleph _1$
since this is true in the final model so we can add the unbounded family. Fix an
![]() $\aleph _1$
-sized R-unbounded family
$\aleph _1$
-sized R-unbounded family
![]() $\{x_\alpha \; | \; \alpha < \omega _1\}$
. Also, enumerate all of the reals as
$\{x_\alpha \; | \; \alpha < \omega _1\}$
. Also, enumerate all of the reals as
![]() $\{y_\alpha \; | \; \alpha < \omega _2\}$
. Let
$\{y_\alpha \; | \; \alpha < \omega _2\}$
. Let
![]() $\{\dot {g}_\alpha \; | \; \alpha < \omega _2\}$
enumerate
$\{\dot {g}_\alpha \; | \; \alpha < \omega _2\}$
enumerate
![]() $\mathbb R$
-names for
$\mathbb R$
-names for
![]() $\omega _2$
many generic functions
$\omega _2$
many generic functions
![]() $\omega _1 \to \omega _1$
. Via a bijection from
$\omega _1 \to \omega _1$
. Via a bijection from
![]() $\omega _2 \times \omega _1$
to
$\omega _2 \times \omega _1$
to
![]() $\omega _2$
, we can think of this as one function from
$\omega _2$
, we can think of this as one function from
![]() $\omega _2$
to
$\omega _2$
to
![]() $\omega _1$
. Let’s name this function
$\omega _1$
. Let’s name this function
![]() $\dot {g}$
. Consider now a name
$\dot {g}$
. Consider now a name
![]() $\dot {g} '$
for the function
$\dot {g} '$
for the function
![]() $g':\omega ^\omega \to \omega ^\omega $
in
$g':\omega ^\omega \to \omega ^\omega $
in
![]() $V[G][H]$
so that
$V[G][H]$
so that
![]() $\dot g'(y_\alpha ) = x_\beta $
if and only if
$\dot g'(y_\alpha ) = x_\beta $
if and only if
![]() $\dot {g}(\alpha ) = \beta $
. The following claim leads to the contradiction which completes the proof.
$\dot {g}(\alpha ) = \beta $
. The following claim leads to the contradiction which completes the proof.
Claim 6.4. In W we have
![]() $\Vdash _{\mathbb R}$
“
$\Vdash _{\mathbb R}$
“
![]() $\dot {g}'$
is not
$\dot {g}'$
is not
![]() $R_{\{\emptyset \}}$
-dominated by the
$R_{\{\emptyset \}}$
-dominated by the
![]() $\dot {f}_\alpha $
’s”.
$\dot {f}_\alpha $
’s”.
Proof of Claim Fix
![]() $\alpha < \omega _3$
, let
$\alpha < \omega _3$
, let
![]() $p \in \mathbb R$
and let
$p \in \mathbb R$
and let
![]() $\gamma < \omega _2$
be so that p does not decide
$\gamma < \omega _2$
be so that p does not decide
![]() $\dot {g}(\gamma )$
. Now we can simply extend p to some q which forces
$\dot {g}(\gamma )$
. Now we can simply extend p to some q which forces
![]() $\dot {g} (\gamma ) = \beta $
so that
$\dot {g} (\gamma ) = \beta $
so that
![]() $x_\beta $
is not R-below
$x_\beta $
is not R-below
![]() $\dot {f}_\alpha (y_\gamma )$
(since
$\dot {f}_\alpha (y_\gamma )$
(since
![]() $\{x_\alpha \; | \; \alpha < \omega _1\}$
is an unbounded family). But then q forces that
$\{x_\alpha \; | \; \alpha < \omega _1\}$
is an unbounded family). But then q forces that
![]() $\dot {f}_\alpha $
is not an
$\dot {f}_\alpha $
is not an
![]() $R_{\{\emptyset \}}$
-bound on
$R_{\{\emptyset \}}$
-bound on
![]() $\dot {g}'$
as desired.
$\dot {g}'$
as desired.
We now begin with the first model towards proving Theorem 6.1.
Lemma 6.5. Assume
![]() $\mathsf {GCH}$
. Let
$\mathsf {GCH}$
. Let
![]() $G \subseteq add(\omega _1, \omega _4)$
be generic over V. Let H be generic for
$G \subseteq add(\omega _1, \omega _4)$
be generic over V. Let H be generic for
![]() $\mathbb B_{\omega _2}$
over
$\mathbb B_{\omega _2}$
over
![]() $V[G]$
. Then in
$V[G]$
. Then in
![]() $V[G][H]$
we have:
$V[G][H]$
we have:
-
(1)
 $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \aleph _3$
.
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \aleph _3$
. -
(2)
 $\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}(\in ^*_{\{\emptyset \}}) = \aleph _4$
.
$\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \mathfrak {d}(\in ^*_{\{\emptyset \}}) = \aleph _4$
.
Proof As in the proof of Lemma 6.3, note that the cardinal arithmetic in this model is
![]() $2^{\aleph _0} = \aleph _2$
and
$2^{\aleph _0} = \aleph _2$
and
![]() $2^{\aleph _1} = 2^{\aleph _2} = 2^{\aleph _3} = \aleph _4$
and by Lemma 6.2,
$2^{\aleph _1} = 2^{\aleph _2} = 2^{\aleph _3} = \aleph _4$
and by Lemma 6.2,
![]() $\mathfrak {d}_{\aleph _1} = \aleph _4$
and
$\mathfrak {d}_{\aleph _1} = \aleph _4$
and
![]() $\mathfrak {d}_{\aleph _2} = \aleph _3$
. It follows that every
$\mathfrak {d}_{\aleph _2} = \aleph _3$
. It follows that every
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
is either
$\mathfrak {d}(R_{\{\emptyset \}})$
is either
![]() $\aleph _3$
or
$\aleph _3$
or
![]() $\aleph _4$
in light of Corollary 5.2. From now on work in
$\aleph _4$
in light of Corollary 5.2. From now on work in
![]() $V[G]$
.
$V[G]$
.
Let us begin by showing that
![]() $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \aleph _3$
. Indeed, it suffices to see that
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \aleph _3$
. Indeed, it suffices to see that
![]() $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) \leq \aleph _3$
since the lower bound is for free in light of Corollary 5.2. However,
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) \leq \aleph _3$
since the lower bound is for free in light of Corollary 5.2. However,
![]() $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) \leq \aleph _3$
actually follows from the first part of Lemma 5.6 given the fact that there is an eventually
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) \leq \aleph _3$
actually follows from the first part of Lemma 5.6 given the fact that there is an eventually
![]() $\neq ^*$
-dominating sequence of length
$\neq ^*$
-dominating sequence of length
![]() $\omega _2$
in the random model.
$\omega _2$
in the random model.
Now we turn to the proof that
![]() $\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _4$
. Since
$\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _4$
. Since
![]() $\mathfrak {d}(\leq ^*_{\{\emptyset \}}) \leq \mathfrak {d}(\in ^*_{\{\emptyset \}}) \leq \aleph _4$
this will complete the proof of the theorem. This however follows from the fact that
$\mathfrak {d}(\leq ^*_{\{\emptyset \}}) \leq \mathfrak {d}(\in ^*_{\{\emptyset \}}) \leq \aleph _4$
this will complete the proof of the theorem. This however follows from the fact that
![]() $\mathfrak b = \aleph _1$
in the random model alongside an application of Lemma 6.3. Alternatively, we can simply use the fact that in the random model there is a scale of length
$\mathfrak b = \aleph _1$
in the random model alongside an application of Lemma 6.3. Alternatively, we can simply use the fact that in the random model there is a scale of length
![]() $\aleph _1$
and apply Lemma 5.7.
$\aleph _1$
and apply Lemma 5.7.
Moving on to the next model we have the following.
Lemma 6.6. Assume
![]() $\mathsf {GCH}$
. Let
$\mathsf {GCH}$
. Let
![]() $G \subseteq add(\omega _1, \omega _4)$
be generic over V. Let H be generic for
$G \subseteq add(\omega _1, \omega _4)$
be generic over V. Let H be generic for
![]() $\mathbb D_{\omega _2}$
, the finite support iteration of length
$\mathbb D_{\omega _2}$
, the finite support iteration of length
![]() $\omega _2$
of Hechler forcing, over
$\omega _2$
of Hechler forcing, over
![]() $V[G]$
. Then in
$V[G]$
. Then in
![]() $V[G][H]$
we have:
$V[G][H]$
we have:
-
(1)
 $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _3$
.
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _3$
. -
(2)
 $\mathfrak {d}(\in ^*_{\{\emptyset \}}) = \aleph _4$
.
$\mathfrak {d}(\in ^*_{\{\emptyset \}}) = \aleph _4$
.
Proof The proof of this theorem is very similar to that of Lemma 6.5. As in that proof, in
![]() $V[G]$
we have that
$V[G]$
we have that
![]() $2^{\aleph _0} = \aleph _2$
and
$2^{\aleph _0} = \aleph _2$
and
![]() $2^{\aleph _1} = 2^{\aleph _2} = 2^{\aleph _3} = \aleph _4$
and by Lemma 6.2
$2^{\aleph _1} = 2^{\aleph _2} = 2^{\aleph _3} = \aleph _4$
and by Lemma 6.2
![]() $\mathfrak {d}_{\aleph _1} = \aleph _4$
and
$\mathfrak {d}_{\aleph _1} = \aleph _4$
and
![]() $\mathfrak {d}_{\aleph _2} = \aleph _3$
. The Hechler reals added form a scale of size
$\mathfrak {d}_{\aleph _2} = \aleph _3$
. The Hechler reals added form a scale of size
![]() $\aleph _2$
(and there is no such scale of size
$\aleph _2$
(and there is no such scale of size
![]() $\aleph _1$
). Again by Lemma 5.7 it follows that
$\aleph _1$
). Again by Lemma 5.7 it follows that
![]() $\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _3$
, which finishes the first item.
$\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _3$
, which finishes the first item.
For the second item we simply apply Lemma 6.3 alongside the fact that
![]() $\mathfrak b(\in ^*)$
is
$\mathfrak b(\in ^*)$
is
![]() $\aleph _1$
in the Hechler model.
$\aleph _1$
in the Hechler model.
Now we consider the model where all three cardinals are different.
Lemma 6.7. Assume
![]() $\mathsf {GCH}$
. Let
$\mathsf {GCH}$
. Let
![]() $G \subseteq add (\omega _2, \omega _5)$
be generic over V. Let
$G \subseteq add (\omega _2, \omega _5)$
be generic over V. Let
![]() $H \subseteq add(\omega _1, \omega _6)$
be generic over
$H \subseteq add(\omega _1, \omega _6)$
be generic over
![]() $V[G]$
. In
$V[G]$
. In
![]() $V[G][H]$
let
$V[G][H]$
let
![]() $\mathbb P$
be the forcing consisting of an
$\mathbb P$
be the forcing consisting of an
![]() $\omega _2$
-length iteration of Hechler forcing followed by adding
$\omega _2$
-length iteration of Hechler forcing followed by adding
![]() $\omega _3$
many random reals,
$\omega _3$
many random reals,
![]() $\mathbb D_{\omega _2} * \dot {\mathbb B}_{\omega _3}$
and let
$\mathbb D_{\omega _2} * \dot {\mathbb B}_{\omega _3}$
and let
![]() $K \subseteq \mathbb P$
be generic over
$K \subseteq \mathbb P$
be generic over
![]() $V[G][H]$
. In
$V[G][H]$
. In
![]() $V[G][H][K]$
we have:
$V[G][H][K]$
we have:
-
(1)
 $\mathfrak {d}(\in ^*_{\{\emptyset \}}) = \aleph _6$
.
$\mathfrak {d}(\in ^*_{\{\emptyset \}}) = \aleph _6$
. -
(2)
 $\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _5$
.
$\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _5$
. -
(3)
 $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \aleph _4$
.
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \aleph _4$
.
Proof Modifying the arguments from Lemmas 6.2 and 6.3 alongside well known facts about these forcing notions we have that in
![]() $V[G][H][K]$
the following all hold.
$V[G][H][K]$
the following all hold.
-
(1)
 $2^{\aleph _0} = \aleph _3$
and for all
$2^{\aleph _0} = \aleph _3$
and for all
 $\kappa \in [\aleph _1, \aleph _5]$
,
$\kappa \in [\aleph _1, \aleph _5]$
,
 $2^{\kappa } = \aleph _6$
,
$2^{\kappa } = \aleph _6$
, -
(2)
 $\mathfrak b(\in ^*) =\aleph _1 < \mathfrak b = \mathfrak {d} = \aleph _2 < \mathfrak b(\neq ^*) = \aleph _3$
, and
$\mathfrak b(\in ^*) =\aleph _1 < \mathfrak b = \mathfrak {d} = \aleph _2 < \mathfrak b(\neq ^*) = \aleph _3$
, and -
(3)
 $\mathfrak {d}_{\aleph _3} = \aleph _4$
,
$\mathfrak {d}_{\aleph _3} = \aleph _4$
,
 $\mathfrak {d}_{\aleph _2} = \aleph _5$
and
$\mathfrak {d}_{\aleph _2} = \aleph _5$
and
 $\mathfrak {d}_{\aleph _1} = \aleph _6$
.
$\mathfrak {d}_{\aleph _1} = \aleph _6$
.
Now, by essentially the same argument as in Lemma 6.3 we get that
![]() $\mathfrak {d} (\in ^*_{\{\emptyset \}}) = \aleph _6$
. To show that
$\mathfrak {d} (\in ^*_{\{\emptyset \}}) = \aleph _6$
. To show that
![]() $\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _5$
we will apply Theorem 5.8. We need to see that
$\mathfrak {d}(\leq ^*_{\{\emptyset \}}) = \aleph _5$
we will apply Theorem 5.8. We need to see that
![]() $\mathfrak {d}^{\aleph _3}_{\aleph _2}$
is
$\mathfrak {d}^{\aleph _3}_{\aleph _2}$
is
![]() $\aleph _5$
. To see why this is true, observe that a simply density argument forces that
$\aleph _5$
. To see why this is true, observe that a simply density argument forces that
![]() $\mathfrak {d}^{\aleph _3}_{\aleph _2} = \aleph _5$
in
$\mathfrak {d}^{\aleph _3}_{\aleph _2} = \aleph _5$
in
![]() $V[G]$
and since the remainder forcing is
$V[G]$
and since the remainder forcing is
![]() $\aleph _2$
-c.c., the set
$\aleph _2$
-c.c., the set
![]() $\omega _2^{\omega _3} \cap V[G]$
forms a dominating family in
$\omega _2^{\omega _3} \cap V[G]$
forms a dominating family in
![]() $\omega _2^{\omega _3}$
while no family of smaller cardinality does.
$\omega _2^{\omega _3}$
while no family of smaller cardinality does.
Finally to show that
![]() $\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \aleph _4$
we can use the same argument as in Lemma 6.5 (but upping each cardinal by one).
$\mathfrak {d}(\neq ^*_{\{\emptyset \}}) = \aleph _4$
we can use the same argument as in Lemma 6.5 (but upping each cardinal by one).
The final two models for proving Theorem 6.1 follow (under
![]() $\mathsf {CH}$
) from Theorem 2.1 alongside well known facts about
$\mathsf {CH}$
) from Theorem 2.1 alongside well known facts about
![]() $\mathfrak {d}_{\aleph _1}$
, see for example [Reference Cummings and Shelah6]. However, they can also be proved in the
$\mathfrak {d}_{\aleph _1}$
, see for example [Reference Cummings and Shelah6]. However, they can also be proved in the
![]() $\neg \mathsf {CH}$
context. In the case that all
$\neg \mathsf {CH}$
context. In the case that all
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
cardinals are greater than
$\mathfrak {d}(R_{\{\emptyset \}})$
cardinals are greater than
![]() $\mathfrak {c}^+$
, we can add
$\mathfrak {c}^+$
, we can add
![]() $\omega _4$
many Cohen subsets to
$\omega _4$
many Cohen subsets to
![]() $\omega _1$
and then
$\omega _1$
and then
![]() $\aleph _2$
many Cohen reals and apply Lemma 6.3, noting that in the Cohen model,
$\aleph _2$
many Cohen reals and apply Lemma 6.3, noting that in the Cohen model,
![]() $\mathfrak b(\in ^*) = \mathfrak b = \mathfrak b(\neq ^*) = \aleph _1$
. In the case where all
$\mathfrak b(\in ^*) = \mathfrak b = \mathfrak b(\neq ^*) = \aleph _1$
. In the case where all
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
cardinals are less than
$\mathfrak {d}(R_{\{\emptyset \}})$
cardinals are less than
![]() $2^{\mathfrak {c}}$
, first force to add
$2^{\mathfrak {c}}$
, first force to add
![]() $\omega _4$
many Cohen subsets to
$\omega _4$
many Cohen subsets to
![]() $\omega _1$
and then force with a finite support iteration of localization forcing
$\omega _1$
and then force with a finite support iteration of localization forcing
![]() $\mathbb {LOC}$
of length
$\mathbb {LOC}$
of length
![]() $\omega _2$
. The resulting generic for the localization iteration will be a sequence of
$\omega _2$
. The resulting generic for the localization iteration will be a sequence of
![]() $\omega _2$
-many slaloms
$\omega _2$
-many slaloms
![]() $\{s_\alpha \; | \; \alpha < \omega _2\}$
which is eventually
$\{s_\alpha \; | \; \alpha < \omega _2\}$
which is eventually
![]() $\in ^*$
-dominating. It follows from the first item in Lemma 5.6 that
$\in ^*$
-dominating. It follows from the first item in Lemma 5.6 that
![]() $\mathfrak {d}(R_{\{\emptyset \}}) \leq \mathfrak {d}^{\mathfrak {c}}_{\aleph _2} = \aleph _3$
and hence all
$\mathfrak {d}(R_{\{\emptyset \}}) \leq \mathfrak {d}^{\mathfrak {c}}_{\aleph _2} = \aleph _3$
and hence all
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
cardinals are
$\mathfrak {d}(R_{\{\emptyset \}})$
cardinals are
![]() $\aleph _3$
. See [Reference Switzer7, Section 3.8] for more on properties of the localization poset.
$\aleph _3$
. See [Reference Switzer7, Section 3.8] for more on properties of the localization poset.
7 Conclusion and open questions
The results of the previous section begin to give a more complete picture of the relations
![]() $R_{\mathcal I}$
and their cardinal characteristics. Nevertheless several open questions remain. We conclude by discussing them. The first question concerns the final inequality between the bounding numbers whose negation does not follow from Figures 1, 2 and yet does not hold in any of the models in Section 4.
$R_{\mathcal I}$
and their cardinal characteristics. Nevertheless several open questions remain. We conclude by discussing them. The first question concerns the final inequality between the bounding numbers whose negation does not follow from Figures 1, 2 and yet does not hold in any of the models in Section 4.
Question 1. Is
![]() $\mathfrak b(\neq ^*_{\mathcal N}) < \mathfrak b(\in ^*_{\mathcal K})$
consistent?
$\mathfrak b(\neq ^*_{\mathcal N}) < \mathfrak b(\in ^*_{\mathcal K})$
consistent?
The issue in providing a model where
![]() $\mathfrak b(\neq ^*_{\mathcal N}) < \mathfrak b(\in ^*_{\mathcal K})$
is consistent is that for most of our consistent inequalities, the smaller one is shown to be
$\mathfrak b(\neq ^*_{\mathcal N}) < \mathfrak b(\in ^*_{\mathcal K})$
is consistent is that for most of our consistent inequalities, the smaller one is shown to be
![]() $\aleph _1$
using Lemma 3.2. However, by Proposition 3.4 this is not possible in this case. Indeed, if
$\aleph _1$
using Lemma 3.2. However, by Proposition 3.4 this is not possible in this case. Indeed, if
![]() ${\textrm {add}}(\mathcal N) < \mathfrak {d}$
then by Lemma 3.2 we have that
${\textrm {add}}(\mathcal N) < \mathfrak {d}$
then by Lemma 3.2 we have that
![]() $\mathfrak b(\in ^*_{\mathcal K}) = {\textrm {add}}(\mathcal N)$
so in such a model
$\mathfrak b(\in ^*_{\mathcal K}) = {\textrm {add}}(\mathcal N)$
so in such a model
![]() $\mathfrak b(\in ^*_{\mathcal K}) \leq \mathfrak b(\neq ^*_{\mathcal N})$
. It follows that if
$\mathfrak b(\in ^*_{\mathcal K}) \leq \mathfrak b(\neq ^*_{\mathcal N})$
. It follows that if
![]() $\mathfrak b(\neq ^*_{\mathcal N}) < \mathfrak b(\in ^*_{\mathcal K})$
is consistent we must have that
$\mathfrak b(\neq ^*_{\mathcal N}) < \mathfrak b(\in ^*_{\mathcal K})$
is consistent we must have that
![]() ${\textrm {add}}(\mathcal N) = \mathfrak {d} < \mathfrak {c}$
, however in all the standard models of this inequality we have computed, namely the random and Sacks models, the inequality
${\textrm {add}}(\mathcal N) = \mathfrak {d} < \mathfrak {c}$
, however in all the standard models of this inequality we have computed, namely the random and Sacks models, the inequality
![]() $\mathfrak b(\neq ^*_{\mathcal N}) < \mathfrak b(\in ^*_{\mathcal K})$
does not hold.Footnote
2
$\mathfrak b(\neq ^*_{\mathcal N}) < \mathfrak b(\in ^*_{\mathcal K})$
does not hold.Footnote
2
The next question we have also concerns the bounding numbers. Recall that the final
![]() $\mathfrak b(R_{\mathcal I})$
number not computed is
$\mathfrak b(R_{\mathcal I})$
number not computed is
![]() $\mathfrak b(\in ^*_{\mathcal M})$
in the Laver model.
$\mathfrak b(\in ^*_{\mathcal M})$
in the Laver model.
Question 2. What is the value of
![]() $\mathfrak b(\in ^*_{\mathcal M})$
in the Laver model?
$\mathfrak b(\in ^*_{\mathcal M})$
in the Laver model?
As noted in the section on the Laver model, this cardinal must be either
![]() $\aleph _2$
or
$\aleph _2$
or
![]() $\aleph _3$
. A related question is the following.
$\aleph _3$
. A related question is the following.
Question 3. Is there an
![]() $(\aleph _2, \aleph _1)$
-Rothberger family for
$(\aleph _2, \aleph _1)$
-Rothberger family for
![]() $\mathcal M$
in the Laver model?
$\mathcal M$
in the Laver model?
Note that a positive answer to this question implies that
![]() $\mathfrak b(\in ^*_{\mathcal M}) = \aleph _3$
in the Laver model by Lemma 3.5.
$\mathfrak b(\in ^*_{\mathcal M}) = \aleph _3$
in the Laver model by Lemma 3.5.
We can also ask about Rothberger families more generally. As noted after the proof of Lemma 3.5, every computation of the form
![]() $\mathfrak b(R_{\mathcal I})> \mathfrak {c}$
can be thought of as factoring through this lemma. It is therefore worth asking if this is necessary.
$\mathfrak b(R_{\mathcal I})> \mathfrak {c}$
can be thought of as factoring through this lemma. It is therefore worth asking if this is necessary.
Question 4. Given R and
![]() $\mathcal I$
, assume
$\mathcal I$
, assume
![]() $\mathfrak b(R_{\mathcal I})> \mathfrak {c}$
. Does it follow that there exists a
$\mathfrak b(R_{\mathcal I})> \mathfrak {c}$
. Does it follow that there exists a
![]() $(\mathfrak {c}, \mathfrak b(R))$
-Rothberger family for
$(\mathfrak {c}, \mathfrak b(R))$
-Rothberger family for
![]() $\mathcal I$
as in Lemma 3.5?
$\mathcal I$
as in Lemma 3.5?
Moving on the dominating numbers, the main open question, as discussed in Section 5 is the relation between the cardinals of the form
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
and the numbers
$\mathfrak {d}(R_{\{\emptyset \}})$
and the numbers
![]() $\mathfrak {d}^\lambda _\kappa $
.
$\mathfrak {d}^\lambda _\kappa $
.
Question 5. Is every
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
cardinal equal to one of the form
$\mathfrak {d}(R_{\{\emptyset \}})$
cardinal equal to one of the form
![]() $\mathfrak {d}_\kappa ^{\mathfrak {c}}$
? In particular, is
$\mathfrak {d}_\kappa ^{\mathfrak {c}}$
? In particular, is
![]() $\mathfrak {d}(R_{\{\emptyset \}})\ \mathsf {ZFC}$
-provably equal to
$\mathfrak {d}(R_{\{\emptyset \}})\ \mathsf {ZFC}$
-provably equal to
![]() $\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b(R)}$
?
$\mathfrak {d}^{\mathfrak {c}}_{\mathfrak b(R)}$
?
One can ask a more general question along these lines. Namely if the cardinal characteristics on spaces of the form
![]() $\kappa ^\lambda $
with
$\kappa ^\lambda $
with
![]() $\kappa \leq \lambda \leq \mathfrak {c}$
determine any of the bounding or dominating numbers for the
$\kappa \leq \lambda \leq \mathfrak {c}$
determine any of the bounding or dominating numbers for the
![]() $R_{\mathcal I}$
relations.
$R_{\mathcal I}$
relations.
Question 6. Are any of the cardinal characteristics discussed determined by the values of the cardinals in the Cichoń diagram and its higher analogues on
![]() $\kappa ^\lambda $
for
$\kappa ^\lambda $
for
![]() $\kappa \leq \lambda \leq \mathfrak {c}$
?
$\kappa \leq \lambda \leq \mathfrak {c}$
?
Put another way, is there either a
![]() $\mathfrak b(R_{\mathcal I})$
or a
$\mathfrak b(R_{\mathcal I})$
or a
![]() $\mathfrak {d}(R_{\{\emptyset \}})$
cardinal whose value is completely determined by the values in the Cichoń diagrams on
$\mathfrak {d}(R_{\{\emptyset \}})$
cardinal whose value is completely determined by the values in the Cichoń diagrams on
![]() $\kappa ^\kappa $
for
$\kappa ^\kappa $
for
![]() $\kappa \in [\omega , \mathfrak {c}]$
and the numbers
$\kappa \in [\omega , \mathfrak {c}]$
and the numbers
![]() $\mathfrak b^\lambda _\kappa $
and
$\mathfrak b^\lambda _\kappa $
and
![]() $\mathfrak {d}^\lambda _\kappa $
for
$\mathfrak {d}^\lambda _\kappa $
for
![]() $\kappa \leq \lambda \leq \mathfrak {c}$
? We know by the computation of
$\kappa \leq \lambda \leq \mathfrak {c}$
? We know by the computation of
![]() $\mathfrak b(\in ^*_{\mathcal M})$
in the
$\mathfrak b(\in ^*_{\mathcal M})$
in the
![]() $\lambda $
-dual random model that this is not true in general, but could it be true for some of the cardinals? Note that a positive answer to Question 5 implies a positive answer to this question in the case of the dominating numbers.
$\lambda $
-dual random model that this is not true in general, but could it be true for some of the cardinals? Note that a positive answer to Question 5 implies a positive answer to this question in the case of the dominating numbers.
Finally we ask about the relationship between the
![]() $\mathfrak b(R_{\mathcal I})$
and the
$\mathfrak b(R_{\mathcal I})$
and the
![]() $\mathfrak {d}(R_{\mathcal I})$
cardinals. These relations were not considered in this paper at all.
$\mathfrak {d}(R_{\mathcal I})$
cardinals. These relations were not considered in this paper at all.
Question 7. Can some
![]() $\mathfrak b (R_{\mathcal I})$
be consistently strictly larger than some
$\mathfrak b (R_{\mathcal I})$
be consistently strictly larger than some
![]() $\mathfrak {d} (R_{\mathcal J})$
?
$\mathfrak {d} (R_{\mathcal J})$
?
The only relation R for which is is not explicitly ruled out by Figures 1 and 2 is the relation
![]() $\neq ^*$
, so really the question is whether there is an ideal
$\neq ^*$
, so really the question is whether there is an ideal
![]() $\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
so that
$\mathcal I \in \{\mathcal N, \mathcal M, \mathcal K\}$
so that
![]() $\mathfrak b(\neq ^*_{\mathcal I})> \mathfrak {d}(\neq ^*_{\{\emptyset \}})$
is consistent.
$\mathfrak b(\neq ^*_{\mathcal I})> \mathfrak {d}(\neq ^*_{\{\emptyset \}})$
is consistent.
Acknowledgements
The first author is partially supported by Grant-in-Aid for Scientific Research (C) 18K03398, Japan Society for the Promotion of Science. The second author would like to thank the Austrian Science Fund (FWF) for the generous support through grant number Y1012-N35.